【整流杂谈(五)】
电路理论中有很多量是具有对偶性的,例如:电压<->电流,电容<->电感……等等。下表取自《电路分析基础李瀚荪第三版中》,42页。
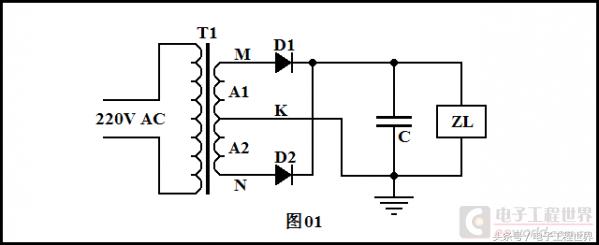
我们曾经谈到过全波整流电容滤波电路,如下图:
此图中整流后的滤波是靠电容C实现的。根据上面的对偶量表,电感和电容是对偶的。那么,是否可以使用电感来滤波?
答案是可以。
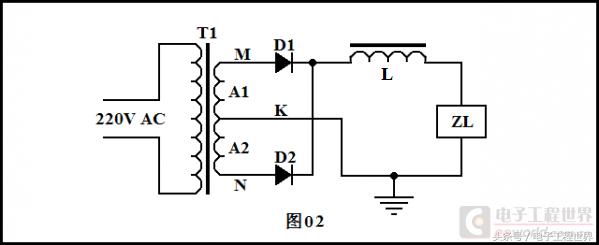
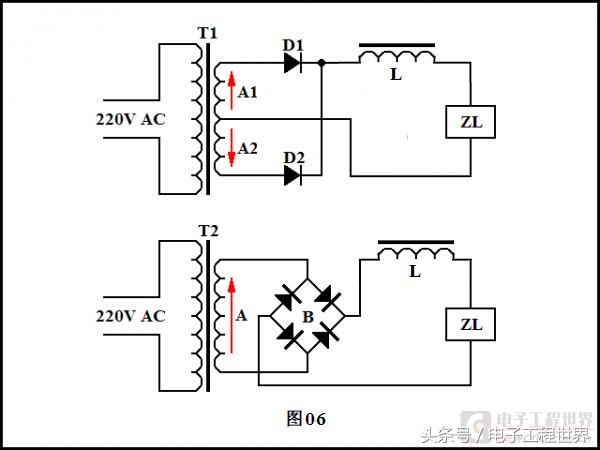
不过,上面的对偶量表里面也明确指出:串联和并联是对偶的。所以使用电感滤波,应该把电感与负载串联起来而不是并联。如下图:
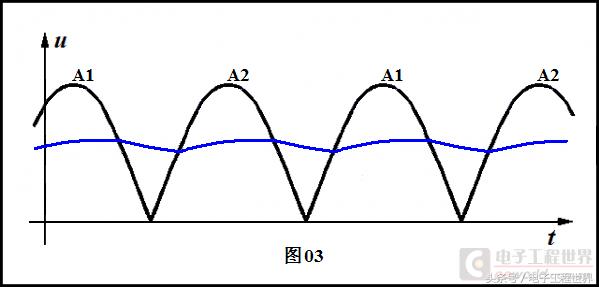
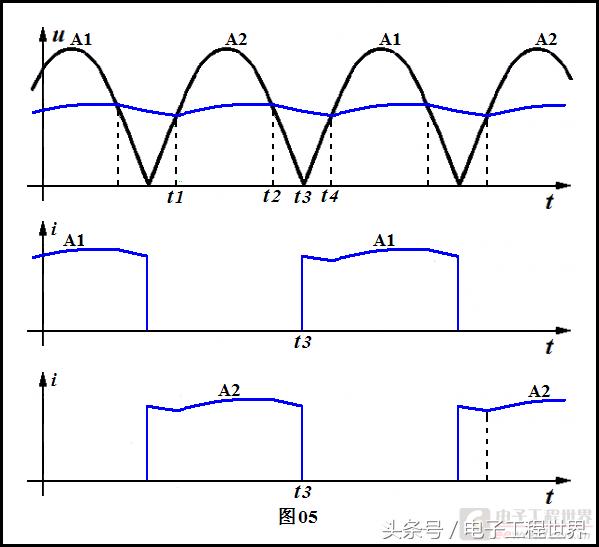
假定电感L比较大(比较大的意思是:电感L的感抗比负载电阻大得多),如果我们用示波器实际观察一下上图中K点电流,将看到如下图中蓝色波形。如果负载ZL是纯电阻,那么负载两端电压波形与通过负载的电流波形同相且成比例(这个比值就是电阻),所以蓝色波形也代表了负载两端电压。图中黑色波形是二极管D1和D2联接处的电压波形。
我们看到,电感滤波电路中电流波形与以前我们谈到过的电容滤波波形很不相同。电容滤波,电流是断续的(见整流杂谈(二)图04),是一个一个的“鼓包”,而电感滤波,电流是连续的(倒是有些像电容滤波的电压波形,这正说明电感与电容、电压与电流的对偶性)。
我们来看看电流是怎样在两个半波绕组中流动的,电流为什么是图03中那个样子。
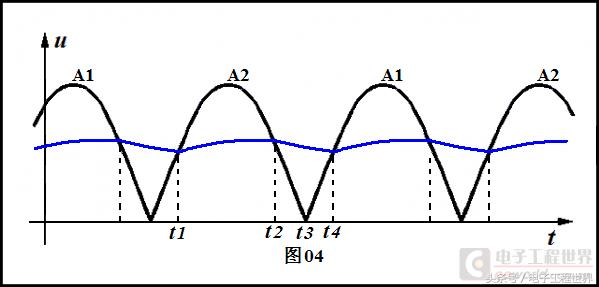
我们从变压器绕组A2两端电压刚好等于此时刻负载两端电压开始,并且忽略二极管正向压降,记此时刻为t1。t1之后变压器绕组A2两端电压大于负载两端电压,那么电感L两端的电压左正右负,电感L中电流增加(蓝色曲线上升),电感储存能量增加。到时刻t2,绕组A2两端电压恰等于负载两端电压,其后绕组A2两端电压小于负载两端电压,电感两端电压左负右正,电感中电流减小,电感所储存的能量释放到负载。绕组A2中电流也就是负载中电流是通过二极管D2构成回路的。
交流过零时刻记为t3。时刻t3之后,变压器次级两端电压反转,二极管D1开始导通,D2关断。电感L和负载中电流从绕组A2和二极管S2转移到绕组A1和二极管D1,电感中和负载电流仍连续。电流从二极管D2转换到D1,这样的过程叫换流。
时刻t4,这个过程重新开始,只不过是这半个周期内是绕组A1在工作。
由上面的叙述,我们可以知道:变压器的两半个次级绕组A1和A2是交替工作的,但电感和负载中的电流却是连续的。交流的每半个周期中,电压较高时电感储存能量,电压较低时电感释放能量到负载。
这样,变压器两个次级绕组中的电流如下图所示,每个绕组中电流都是在半个周期中流动,电流波形接近于矩形。
由计算可知:如果电感比较大,整流并经电感滤波后负载两端直流电压在理想情况(忽略变压器绕组压降和整流管压降以及电感的直流压降)下,为变压器次级半个绕组电压有效值的0.9倍。
图01中的电容滤波电路,负载电阻越大(电流越小),纹波越小。图02中的电感滤波电路,负载电阻越小(电流越大),纹波越小。原因是非常明显的:电容滤波靠的是电容与负载并联,负载电阻越大,相比较之下容抗越小,纹波成份将主要从电容中流过。电感滤波靠的是电感与负载串联,负载电阻越小,相比较之下感抗越大,纹波成份将主要降落在电感上。
和全波整流电容滤波变压器次级电流波形(见整流杂谈(三)图02)相比较,可以看出来:电感滤波变压器绕组中电流波形的波形系数比较小,也就是说,有效值和平均值之比比较小。
上面我们介绍的是全波整流。如果是桥式整流,使用电感滤波,那么电感的工作与全波整流完全相同,负载两端的电压波形也完全相同,不同的仅仅是变压器绕组中在交流电的两半个周期中都有电流,是双向的。桥式整流虽多用两支二极管,但波形系数比全波整流更小,变压器的利用率更高。如下图。
既然电感滤波电路中变压器绕组电流的波形系数比电容滤波电路要小,那么输出同样的直流功率,电感滤波电路所使用的变压器容量是否可以比电容滤波电路所使用的变压器小一些呢?
要输出同样的直流功率,电感滤波电路所使用的变压器容量确实可以比电容滤波电路所使用的变压器容量小一些,几乎可以小一半。但是,变压器体积重量等等的减小,很可能被滤波电感的体积重量所抵消。要知道滤波电感也是具有铁芯和绕组的一个比较大也比较重的东西。
回到本帖开始那张表。那表告诉我们:在电路中,电感和电容是对偶的,串联和并联是对偶的,电压和电流是对偶的。我们又知道,图01中,由于电容C的充电和放电,使得C两端电压基本保持稳定,对负载来说,电容C近似一个电压源,意思就是:负载有比较小的突然变化时,两端电压基本不变。
那么,如图02的电感滤波,对负载来说,是否仍是一个电压源?还是依照本帖开始的表,它应该是对偶的电流源?
我们只需要考察一下当负载有比较小的突然变化时,是负载两端电压不变还是流过负载的电流不变即可。
图02中,流过负载的电流就是流过电感的电流。所以,可以肯定地说,当负载ZL有个比较小的突然变化时,由于电感要保持其中的电流不变,所以流过负载的电流也不变。对负载来说,这是一个电流源,或者说,从负载两端向左看过去,是个电流源。
这样的电流源,在负载突然变轻(负载电阻突然变大)时,负载两端电压会突然上升。这种特性对多数电子设备来说是不允许的。
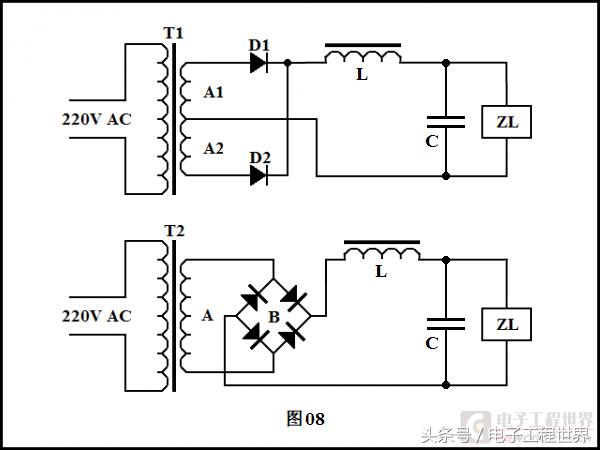
由于大多数直流用电设备要求两端电压不变,所以图02并不能直接使用,往往要在负载两端并联一支比较大的电容C,如图08,以使变压器、整流、滤波部分成为对负载来说是近似的电压源。这就成了所谓LC滤波电路。这种LC滤波电路,在很老式(上个世纪40年代)的真空管收音机和小型发射机中用得相当多。
负载并联上电容C之后,我们看到电感L和电容C是串联关系。这是不是构成了LC串联谐振电路?要知道,串联谐振电路在谐振时,电容或者电感两端电压可以大于供电电压,甚至大上很多倍。
电感L和电容C确实构成LC串联谐振电路。不过,是否发生串联谐振,那还要看信号源(图08中就是整流输出)频率是否等于该谐振电路的固有频率。
工频是50Hz,整流后含很多频率,其中基波频率是100Hz。如果LC串联后的固有频率恰为100Hz,那么就会发生谐振,如果LC回路的Q值稍高,电感L两端和电容C两端电压也可能变得相当高,此时电容C可能被击穿,更可能损坏负载。
所以,电感L和电容C的电感量和电容量数值,务必不能使该电路固有频率落到100Hz上,甚至落到100Hz附近都不行(事实上此时也没有滤波作用),一定要让L和C固有频率落到远低于50Hz,例如5Hz以下。即使如此,负载变化的频率(例如手动控制一个电热器不断开关,这也是一种扰动)也不能落到电感L和电容C串联后的固有频率附近,那也会发生谐振,可能会使电感L和电容C两端电压变得相当高。二战时美国和苏联生产的军用小型报话两用电台,通话时不存在因负载变化而使LC滤波电路发生谐振的问题,因为语音不可能包括数Hz的频率,但发送电报时就有这个问题。当时还是人工电报,手动按键发报的频率就是数Hz,会引起LC滤波电路发生谐振。为避免电感和电容两端电压过高,不得不在电感两端并联一支电阻来增加损耗,以降低LC回路的Q值。电子设备中电感电容滤波使用得比较少,这也是原因之一。
那么,在负载ZL两端并联了电容C之后,负载两端电压倒底是书上说的:电容滤波负载两端电压最大为变压器绕组电压有效值的1.414倍?还是本帖图05前面那段所说的变压器绕组电压有效值的0.9倍?
这个问题比较复杂,不但和电感量有关,还和负载电阻有关。由于本文不拟使用较多数学列式计算,所以只作定性说明:电感中电流连续(没有电流为零的时刻),负载两端电压就能够保持次级绕组电压有效值的0.9倍。当电感中电流不连续时,负载两端电压会升高,接近电容滤波。显然,电感量越小,负载电阻越大,越接近于电容滤波。
转载请注明:徐自远的乱七八糟小站 » 【整流杂谈(五)】