链接:https://www.zhihu.com/question/34170804/answer/121533317

来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
本科毕业设计做的点云配准,对这个方面有一些初步理解,希望有所帮助~
1、首先,点云配准过程,就是求一个两个点云之间的旋转平移矩阵(rigid transform or euclidean transform 刚性变换或欧式变换),将源点云(source cloud)变换到目标点云(target cloud)相同的坐标系下。
可以表示为以下的方程:
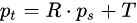
其中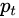
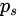 就是target cloud与source cloud中的一对对应点。
就是target cloud与source cloud中的一对对应点。
而我们要求的就是其中的R与T旋转平移矩阵。
这里,我们并不知道两个点集中点的对应关系。这也就是配准的核心问题。
2、配准分为粗配准与精配准两步。
粗配准就是再两个点云还差得十万八千里、完全不清楚两个点云的相对位置关系的情况下,找到一个这两个点云近似的旋转平移矩阵(不一定很精确,但是已经大概是对的了)。
精配准就是在已知一个旋转平移的初值的情况下(这个初值大概已经是正确的了),进一步计算得到更加精确的旋转平移矩阵。
这里从精配准开始讲起。
精配准的模式基本上已经固定为使用ICP算法及其各种变种。ICP算法由Besl and McKay 1992, Method for registration of 3-D shapes文章提出。文中提到的算法不仅仅考虑了点集与点集之间的配准,还有点集到模型、模型到模型的配准等。
简要介绍一下点集到点集ICP配准的算法:
1)ICP算法核心是最小化一个目标函数:
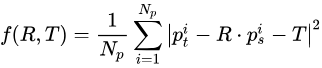
(这里的表述与原文略微有些不同,原文是用四元数加上一个偏移向量来表达旋转平移变换。)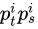 就是一对对应点,总共有
就是一对对应点,总共有 对对应点。这个目标函数实际上就是所有对应点之间的欧式距离的平方和。
对对应点。这个目标函数实际上就是所有对应点之间的欧式距离的平方和。
2)寻找对应点。可是,我们现在并不知道有哪些对应点。因此,我们在有初值的情况下,假设用初始的旋转平移矩阵对source cloud进行变换,得到的一个变换后的点云。然后将这个变换后的点云与target cloud进行比较,只要两个点云中存在距离小于一定阈值(这就是题主所说的ICP中的一个参数),我们就认为这两个点就是对应点。这也是”最邻近点”这个说法的来源。
3)R、T优化。有了对应点之后,我们就可以用对应点对旋转R与平移T进行估计。这里R和T中只有6个自由度,而我们的对应点数量是庞大的(存在多余观测值)。因此,我们可以采用最小二乘等方法求解最优的旋转平移矩阵。一个数值优化问题,这里就不详细讲了。
4)迭代。我们优化得到了一个新的R与T,导致了一些点转换后的位置发生变化,一些最邻近点对也相应的发生了变化。因此,我们又回到了步骤2)中的寻找最邻近点方法。2)3)步骤不停迭代进行,直到满足一些迭代终止条件,如R、T的变化量小于一定值,或者上述目标函数的变化小于一定值,或者邻近点对不再变化等。(这里也是题主所说的ICP算法中的一个参数)
算法大致流程就是上面这样。这里的优化过程是一个贪心的策略。首先固定R跟T利用最邻近算法找到最优的点对,然后固定最优的点对来优化R和T,依次反复迭代进行。这两个步骤都使得目标函数值下降,所以ICP算法总是收敛的,这也就是原文中收敛性的证明过程。这种优化思想与K均值聚类的优化思想非常相似,固定类中心优化每个点的类别,固定每个点的类别优化类中心。
关于参数的选择:
ICP算法的参数主要有两个。一个是ICP的邻近距离,另外一个是迭代的终止条件。这些参数的选择,与实际的工程应用相关。比如说你的仪器精度是5mm,那么小于5mm是可以认为是对应点,而最终的迭代终止条件也就是匹配点之间平均距离小于5mm。而且这些参数可以由算法逐步迭代减小,最初使用较大的对应点距离参数,然后逐步减小到一个较小的值。(问过师兄才知道实际过程这样操作会比较合适。)需要手动调整一些参数。(这跟机器学习调参比起来,简直不是事~~)
3、粗配准
前面介绍到了,ICP算法的基本原理。它需要一个旋转平移矩阵的初值。这个初值如果不太正确,那么由于它的greedy优化的策略,会使其目标函数下降到某一个局部最优点(当然也是一个错误的旋转平移矩阵)。因此,我们需要找到一个比较准确的初值,这也就是粗配准需要做的。
粗配准目前来说还是一个难点。针对于不同的数据,有许多不同的方法被提出。
我们先介绍配准的评价标准,再在这个标准下提出一些搜索策略。
评价标准:比较通用的一个是LCP(Largetst Common Pointset)。给定两个点集P,Q,找到一个变换T(P),使得变换后的P与Q的重叠度最大。在变换后的P内任意一点,如果在容差范围内有另外一个Q的点,则认为该点是重合点。重合点占所有点数量的比例就是重叠度。
解决上述LCP问题,最简单粗暴的方法就是遍历。假设点集P,Q的大小分别为m,n。而找到一个刚体变换需要3对对应点。那么brute force 搜索的需要的复杂度。对于动辄几百万个点的点云,这种时间复杂度是不可接受的。因此,许多搜索策略被提出。比较容易想到的是RANSAC之类的搜索方法。而对于不同的场景特点,可以利用需配准点云的特定信息加快搜索。(例如知道点云是由特定形状的面构成的)这里先介绍一个适用于各种点云,不需要先验信息的搜索策略,称为4PC(4 Point Congruent)。
搜索策略:4PC搜索策略是在P,Q中找到四个共面的对应点。

如上图所示(来自4PC原文),这四个共面的点相交于e。这里有两个比例在刚体变化下是不变的。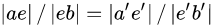
 (实际上在仿射变换下也是不变的。)
(实际上在仿射变换下也是不变的。)
而4PC将对于三个点的搜索转换为对e,e’的搜索,从而将复杂度降低到了 。这四个点的距离越远,计算得到的转换越稳健。但是这里的四个点的搜索依赖于两个点云的重叠度。
。这四个点的距离越远,计算得到的转换越稳健。但是这里的四个点的搜索依赖于两个点云的重叠度。
具体的算法可以参考4-Points Congruent Sets for Robust Pairwise Surface Registration的原文。4PC算法通用性较好,但是对于重叠度较小、或是噪声较大的数据也会出现配准错误或是运行时间过长的问题。针对于不同的场景很多其他的搜索策略也被提出。
这里安利一下我师兄的论文吧~Automatic registration of large-scale urban scene point clouds based on semantic feature points
我们课题组主要是研究室外地面站LiDAR获取的点云配准问题。这种情形下,由于扫描仪内有自动安平装置,Z轴都是竖直方向(重力方向),刚体变换只存在三维平移与平面(XoY面上的)旋转。我们就在场景中搜索竖直的特征线并且得到它们与地面的交点。

再将这些交点构建出三角形,以三角形的全等关系来得到匹配。
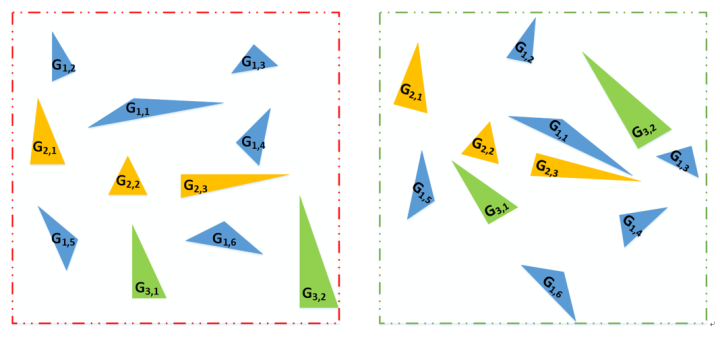
找出其中一致性最好的三角形集合,作为匹配的集合,进行粗配准。这种方法适用于竖直线较多的场景,比如城区的建筑物的边线、林区树木的树干等。设计的方法还是很巧妙的。当然如果场景内这种特征较少,就比较难以配准。
(填坑完成~)
参考文献:
[1] Besl P J, Mckay N D. Method for registration of 3-D shapes[C]// Robotics – DL tentative. International Society for Optics and Photonics, 1992:239-256.
[2] Aiger D, Mitra N J, Cohen-Or D. 4-points congruent sets for robust pairwise surface registration[J]. Acm Transactions on Graphics, 2008, 27(3):85.
[3]Yang B, Dong Z, Liang F, et al. Automatic registration of large-scale urban scene point clouds based on semantic feature points[J]. Isprs Journal of Photogrammetry & Remote Sensing, 2016, 113:43-58.
更多回答
随着激光雷达,RGBD相机等3D传感器在机器人,无人驾驶领域的广泛应用。针对三维点云数据的研究也逐渐从低层次几何特征提取(PFH,FPFH,VFH等)向高层次语义理解过渡(点云识别,语义分割)。与图像感知领域深度学习几乎一统天下不同,针对无序点云数据的深度学习方法研究则进展缓慢。分析其背后的原因,不外乎三个方面:
1.点云具有无序性。受采集设备以及坐标系影响,同一个物体使用不同的设备或者位置扫描,三维点的排列顺序千差万别,这样的数据很难直接通过End2End的模型处理。
2.点云具有稀疏性。在机器人和自动驾驶的场景中,激光雷达的采样点覆盖相对于场景的尺度来讲,具有很强的稀疏性。在KITTI数据集中,如果把原始的激光雷达点云投影到对应的彩色图像上,大概只有3%的像素才有对应的雷达点。这种极强的稀疏性让基于点云的高层语义感知变得尤其困难。
3.点云信息量有限。点云的数据结构就是一些三维空间的点坐标构成的点集,本质是对三维世界几何形状的低分辨率重采样,因此只能提供片面的几何信息。
面对以上困难,来自斯坦福大学的学者提出了PointNet,给出了自己的的解决方案。PointNet是第一种直接处理无序点云数据的深度神经网络。一般情况下,深度神经网络要求输入信息具有规范化的格式,比如二维的图像,时序性的语音等。而原始的三维点云数据往往是空间中的一些无序点集,假设某一个点云中包含N个三维点,每一个点用(x,y,z)三维坐标表示,即使不考虑遮挡,视角等变化,单就这些点的先后顺序排列组合,就有N!种可能。因此,我们需要设计一个函数,使得函数值与输入数据的顺序无关。实际上,在代数组合学中,这类函数被称为对称函数。PointNet中,作者使用了Max Pooling层做为主要的对称函数,这种处理虽然简单,但是实验证明效果较好。
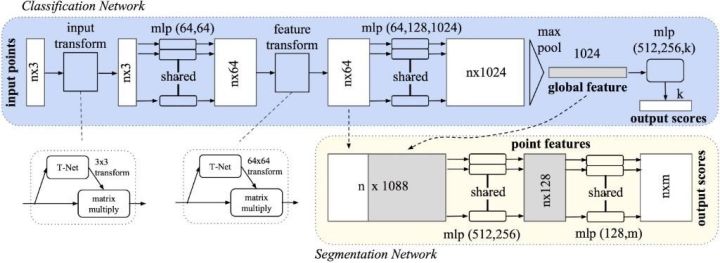
上图是PointNet的网络架构,输入是包含n个点的三维点云(nx3),原始数据通过一个3D空间变换矩阵预测网络T-Net(3),估计出3×3的变换矩阵T(3)并作用在原始数据上,实现数据的对齐。对齐后的数据会以点为单位,通过一个共享参数的双层感知机模型进行特征提取。每个点提取出64维的特征,再通过特征空间变换矩阵预测网络T-Net(64)预测64×64的变换矩阵,作用到特征上,实现对特征的对齐。然后继续利用三层感知机(64,128,1024)进行以特征点为单位的特征提取,直到把特征的维度变为1024,继而在特征空间的维度上进行Max Pooling,提取出点云的全局特征向量。在点云分类任务中,可直接利用特征向量训练SVM或者多层感知机来进行分类,而在以点为单位的点云分割或者分块任务中,需要结合每一点的局部特征和全局特征进行特征融合和处理,实现逐点的分类。PointNet中把经过特征对齐之后的64维特征看成是点的局部特征,把最后的1024维特征看成是点的全局特征,因此通过一个简单的拼接,把局部和全局的特征捆绑在一起,利用多层感知机进行融合,最后训练分类器实现逐点的分类。
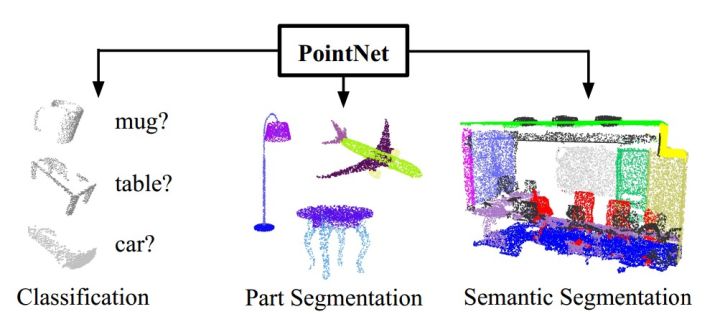
PointNet是第一个可以直接处理原始三维点云的深度神经网络,这种新颖的网络设计可以直接对原始点云进行处理,进而完成高层次的点云分类和语义分割的任务,而且完全依赖于数据。从实验验证的结果来看,其效果和当前最好的结果具有可比性,在一些方面甚至超过了state-of-the-art.值得进一步挖掘和研究。
Q1:输入的原始三维点云数据需要做归一化吗?
答:和其他网络的输入一样,输入点云数据需要做零均值的归一化,这样才能保证比较好的实验性能。
Q2:深层神经网络处理三维离散点云的难点在哪里?PointNet是如何解决这些难点的?
答:深度神经网络处理三维离散点云数据的难点主要在于点云的无序性和输入维度变化。在本篇文章中,我使用了深度神经网络中的常用对称函数:Max Pooling来解决无序性问题,使用共享网络参数的方式来处理输入维度的变化,取得了比较好的效果。
Q3:是否可以使用RNN/LSTM来处理三维点云数据?
答:RNN/LSTM可以处理序列数据,可以是时间序列也可以是空间序列。因此从输入输出的角度来讲,他们可以用来处理三维点云数据。但是点云数据是无序的,这种点和点之间的先后输入顺序并没有规律,因此直接使用RNN/LSTM效果不会太好。
Q4:T-Net在网络结构中起的本质作用是什么?需要预训练吗?
答:T-Net是一个预测特征空间变换矩阵的子网络,它从输入数据中学习出与特征空间维度一致的变换矩阵,然后用这个变换矩阵与原始数据向乘,实现对输入特征空间的变换操作,使得后续的每一个点都与输入数据中的每一个点都有关系。通过这样的数据融合,实现对原始点云数据包含特征的逐级抽象。
Q5:PointNet与MVCNN的实验结果比较中,有些指标稍差,背后的原因是什么?
答:PointNet提取的是每一个独立的点的特征描述以及全局点云特征的描述,并没有考虑到点的局部特征和结构约束,因此与MVCNN相比,在局部特征描述方面能力稍弱。面对这样的问题,我们基于PointNet已经做了一些改进和提升,新的网络命名为 PointNet++,已经上传到Arxiv,欢迎大家阅读并讨论交流。
【自动驾驶公司Momenta2019校园招聘正式启动!点击查看详情】
与我们一同打造更好的人工智能,创造更好的生活,成就更好的你!
成就下一个伟大 | 自动驾驶公司Momenta校园招聘正式启动
————————————————
知乎机构号:Momenta,打造自动驾驶大脑。
基于深度学习的环境感知、高精度地图、驾驶决策技术,让无人驾驶成为可能。
Momenta
知乎专栏:Paper Reading,集聚自动驾驶知名大咖的前沿知识分享平台,欢迎申请加入或直接投稿。

转载请注明:徐自远的乱七八糟小站 » 该如何学习三维点云配准的相关知识?

