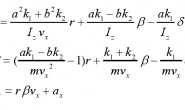从信号处理看卷积

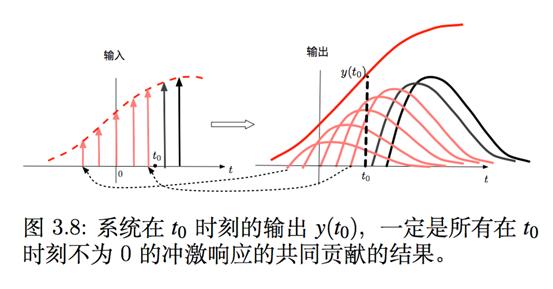
从信号处理的角度则更好理解：h(t)是“冲激响应”，f(t)和h(t)的卷，相当于将f(t)倍数的一堆“h(t)”进行“叠加”，如图3.8。

卷积图解

其实，生活中的卷积，无处不在，更好理解。

比如，人生病了去医院，大夫开药后会叮嘱一句：要按时吃药。

为什么要按时吃药

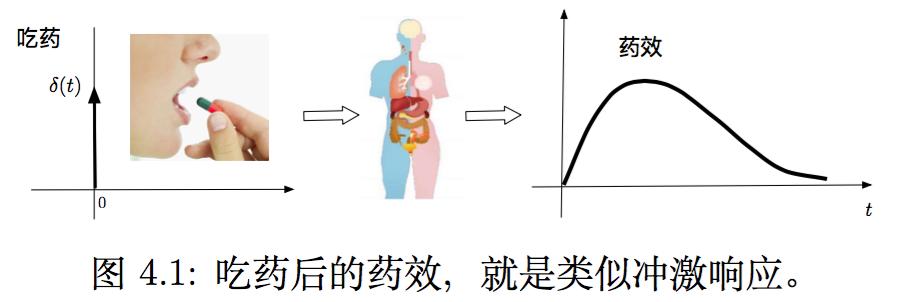
人在t = 0时刻嗑下药，就好比对身体输入了一个冲激函数δ(t)。

而对于这个输入，系统的输出是药效，其大小变化规律，就类似于一个典型的冲激响应：

药效从0开始逐渐增大，到某一时刻到达最大值，然后药效慢慢下降为0。

药效曲线

注意，这是单次吃药（激励）对身体的药效（响应）。

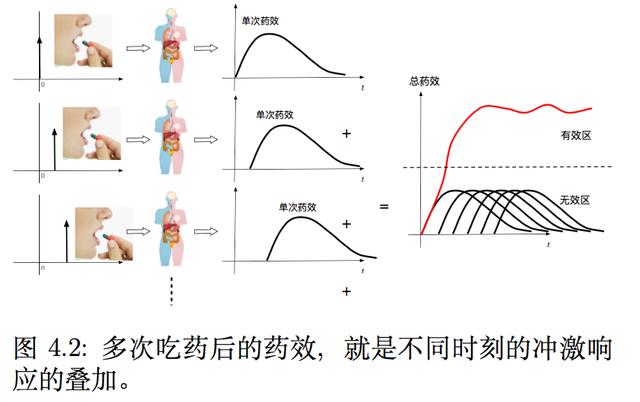
如果我们把人的身体看作一个线性时不变系统的话，显然，多次吃药，就是在不同时间单次吃药的药效的叠加。

如果遵医嘱定时吃药，那么总的药效就类似图4.2中显示的总药效。

定时服药的总药效

此时，总的药效y(t)

y(t) = f(t) * h(t)

h(t)就是一次吃“单位剂量”所产生的药效，即药对人体这个系统的“冲激响应”，f(t)就是每次“剂量大小”。

原则上都是吃同样的“单位剂量”，即每次服药的药效“贡献”都是相同的。

如果想有持续较好的疗效，总的药效，必须在某一个有效区内持续维持一定的水平。

因此，我们必须定时定量吃药，否则，某一次药忘了吃，那么，药效就会迅速跌出有效区，而导致病症反复。

该吃药了。。。

欢迎订阅“卷积精讲”专栏内容，深入浅出，弄懂卷积与卷积神经网络

https://m.toutiao.com/column/v2/index/text_article/landing/?article_id=6597575368406729230