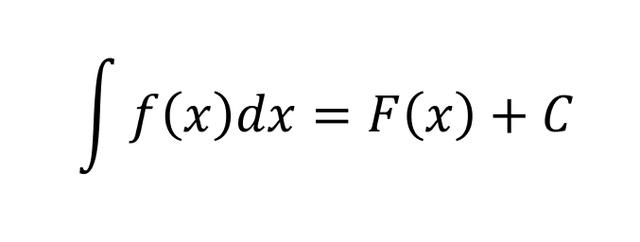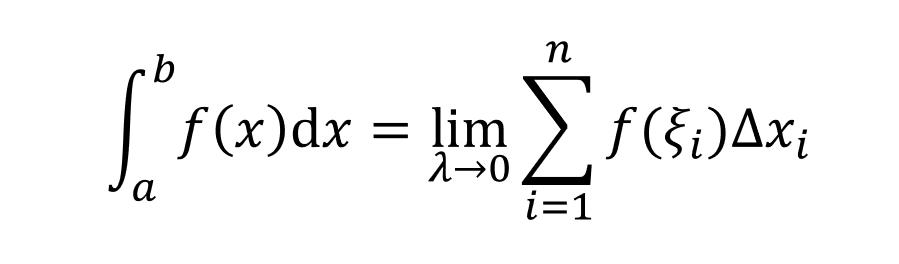微积分其实很简单!
只有理解,才会应用!
本专栏将和您一起,从最通俗易懂的角度,用最易于理解的方法,真正内化吸收微积分的核心概念与算法,帮您轻松掌握与应用!
前两课我们首先讲了导数/微分:
导数的“导”,理解为“方向”。
方向决定了函数的运行,所以“导数”是函数的原因,函数是“导数”的结果。
进一步,借助泰勒展开公式加深了对导数“原因”作用的认识。
泰勒展开公式,是对展开点附近的函数,进行的一个“误差可控多项式仿真”。
函数 F(x) 的导函数为 F'(x),如果定义 F'(x)=f(x),则:
f(x) 是 F(x) 的导函数;
F(x) 是 f(x) 的原函数。
这里注意,F(x) +C 的导数也是 f(x),所以
f(x) 有一族原函数—— F(x) +C
(C在数学里表示常数,常数的导数为0)
表示为:
等号左边那堆,叫做 f(x) 的“不定积分”。
为啥“不定”呢?
主要是为了相对于下面要讲的“定积分”,而且不定积分有“一族”而不是“一个”(下面会讲)。
思考一个问题,为什么从原函数 F 到 导函数 f ,没有常数C的出现;而从导函数 f 到原函数 F 就突然多出来一个 常数 C 呢?
因为,原函数与导函数不在一个维度上!
维度不同,角度完全不同!
原函数比导函数低一个维度!
为什么这么说?
举个例子,一个灯下的三维物体,比如如一个橄榄球,向墙面上的投影可能是一个椭圆,但是换一个角度再去投影,影子完全可能是另一个大小/形状,有可能变成一个圆形!
即,三维物体有无穷多个二维的投影。
正如,导函数有无穷多个原函数!
低维的原函数 是 高维的导函数 的投影。
投影,将三维信息降为了二维信息
常数 C ,就是代表灯与物所成的一系列角度罢了。
原因(导函数)在高维,比如小车的速度 v,这是本身一个高维的信息,因为它:
- 决定了低维信息位移 s;
- “不直观”,如果不投影低维的位移信息,我们甚至不易理解;
- 表达简单,“高维的表达反而简单”。
第三条详细解释一下,这个原理叫:
高维低阶
举个例子,位移 s=x^2 +x+1,则速度v=2x+1。
发现什么了?v比s的阶低,v是1次多项式,s是2次多项式。
高维下的表达,往往就比低维下简单!
二维到三维,是工程制图的升维飞跃
学过工程制图的同学深有体会,一个复杂结构,如果画在平面图中,需要有:正视图/左视图/上视图/甚至斜视图/剖面图等等,特别复杂,但如果在三维作图软件中作三维模型,一个模型就足够了。
就是这个道理。
物理学发展史中,这样的故事层出不穷。最开始探索的物理学家的理解比较浅也比较局限,提出的理念往往很复杂,后来的物理学家在他们基础上,统一整合了一类理论,提出新的理论反而是形式简洁美妙,这就是升维思维的奇功。
简洁的物理公式,其实是最高级的
不定积分,在数学上最大的意义就是求原函数,手算方法很多:
换元积分法 分部积分法 等
教材上都一样,咱们直接用MATLAB解决问题:
|
1 2 |
F=int(fun,x) % 求函数fun关于x的不定积分 |
SO EASY!
提问,如何求一个曲线 f(x) 下包围的面积?
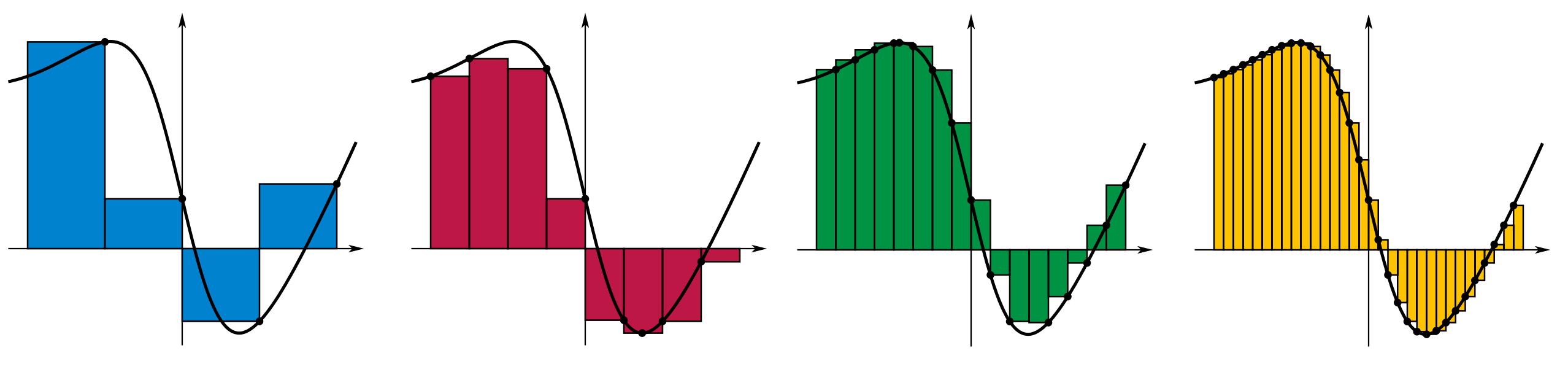
我们采用分割法,把曲线下分割成许多小矩形,如图:
当分割得越来越小,面积就越来越接近真实值。
然后把它们加起来,这就是“定积分”。
这就是定积分在书本上的定义,从中也能看出,积分其实就是求和,你看积分号长得就像一个拉长的 S 啊,S就是 sum 呗!
定积分到底在算啥?
理解微积分真谛:积分——降维投影http://t.zijieimg.com/Qk2qnv/
转载请注明:徐自远的乱七八糟小站 » 理解微积分真谛:积分——降维投影