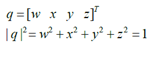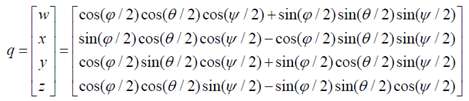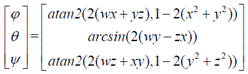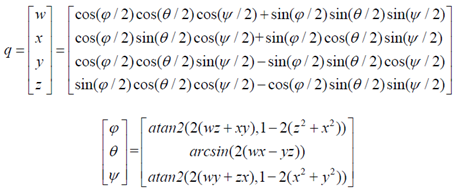★★★★★★★★注意：6050有上电3秒自校准（需写程序）★★★★★★★

注意事项（需要写程序自校准，考虑考虑）
（1）模块上电自校正，需保持3秒以上静止状态，建议不要用手拿着模块；
（2）角度欧拉角由于万向锁问题，横滚，俯仰在90度时候会有相互影响；
（3）右边焊点引脚接地，重启后模块进入 IIC 模式，客户可自行操作传感 器，模块 MCU 不对传感器进行任何操作；

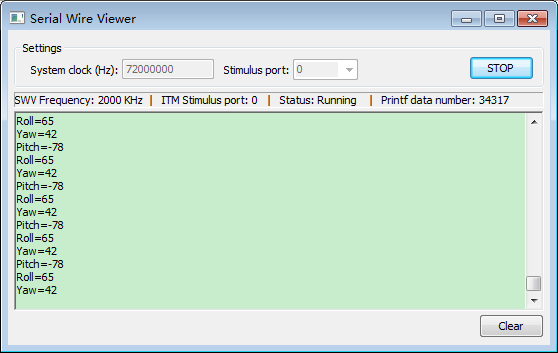
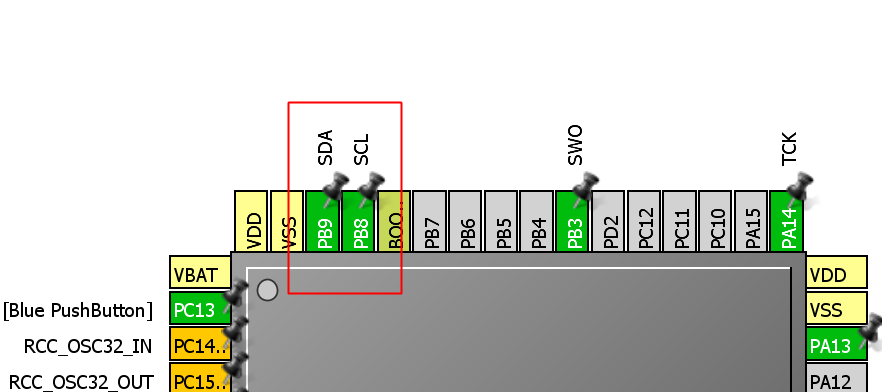
接到一个项目需要做角度计量仪的，准备用九轴来输出角度信息。应该会方便一点。

MPU6050：
SCL–>PB8
SDA–>PB9
ADO–>GND

参考论坛上的这篇文章把6050输出姿态调通了。非常感谢。

http://www.stmcu.org/module/forum/thread-599730-1-1.html

不过源程序中有一个错误，在I2C read中有一个    == 写成了=。其他还有若干错误已在程序中改正。

在调试的时候碰到一个问题，使用sys作为时钟源的时候，程序总死在

HAL_DELAY()延时程序中，后来把timebase 源改为TIM7就好了，不知道为什么。。。。。★手动标记疑问★

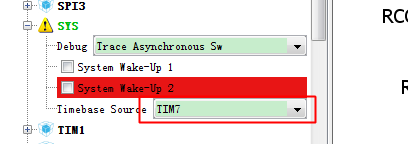
可能是F303的CUBEMX库的bug吧。不准备细究了。

★对了，还有一个傻瓜问题，就是需要把模拟IIC的管脚配置为OD。之前老输出不了就是因为这个缘故。

输出了欧拉角后，利用翻滚角作为角度测量仪的信号输出，其问题是-180~+180°输出的问题，当前角度应该通过换算，最后输出+5v~-5V电压，且极性需要可变。准备利用DA+运放来做。

程序在这里：

打个标记科普一下欧拉角知识：

pitch（倾斜角）y轴旋转（对应模块）

yaw（偏航角）z轴旋转（对应模块）

roll（翻滚角）x轴旋转(对应模块)

关于旋转永远是做游戏的难点和混乱点。我们知道表示一个旋转有多种方式，简单的欧拉角，复杂点的四元数，再复杂点的矩阵。之前接触unity可以用四元数和欧拉角两种方式表示旋转，最近一直研究虚幻引擎，目前只看到了欧拉角这一种旋转方式。

欧拉角是表达旋转的最简单的一种方式，形式上它是一个三维向量，其值分别代表物体绕坐标系三个轴(x,y,z轴）的旋转角度。这样的话，很容易想到，同样的一个三维向量，代表了绕x，y，z的旋转值，先进行那个旋转是否对结果有影响呢？显然是有影响的，可以拿着你的手机试一下，不同的旋转顺序会代表不同的旋转结果。所以，一般引擎都会规定自己的旋转顺序。
下面三张动图形象的表示了欧拉角的旋转方式。第一张是绕x轴旋转pitch，第二张绕y轴旋转yaw，第三张是绕z轴旋转roll。

pitch（倾斜角）

yaw（偏航角）

roll（翻滚角）★本项目应该采用翻滚角ROLL，所以应该保持6050的水平安装。

注意：在这边需要注意的是经过测试，将6050垂直90安装后，ROLL会测量不准，而且垂直90后倾角应该取yaw偏航角而不是翻滚角，但是6050偏航角会随着时间漂移，这就比较麻烦了，所以正式制作电路板时准备做一个90°的转接板，将6050插焊在PCB主板上。

绕三个轴的旋转值pitch，yaw，roll来自航空界的叫法，翻译为俯仰角，偏航角，翻滚角，非常形象。它们不一定如上所述，一定分别代表绕x，y，z的旋转值。
从英文意思出发，roll:是卷；滚动，转动；辗的意思；
yaw是（火箭、飞机、宇宙飞船等）偏航的意思；
pitch是倾斜；投掷；搭帐篷；坠落的意思；
所以，roll的意思是翻滚，就是绕着机身所在的那个轴。yaw是偏航的意思，偏航就是绕着重力方向为轴。pitch倾斜、坠落的意思，坠落就是以翅膀所在的直线为轴发生旋转。

另外值得注意的是，pitch值是不能超过90度，这里牵扯到了万向锁的知识，不再多说，网上很多讨论。

下面这张图是以摄像机的角度来阐述欧拉角的，可以加深理解。可以看到，pitch，yaw，roll在这里并不是常见的代表绕x，y，z的旋转值。

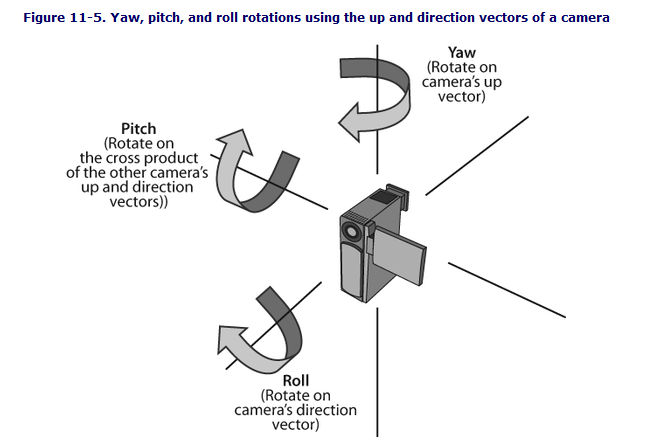
直接计算出roll角度之后就可以使用了。这边还需要注意的是，需要对翻滚角进行校零。

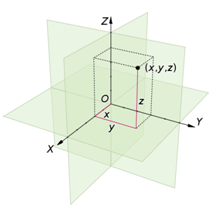
在3D图形学中，最常用的旋转表示方法便是四元数和欧拉角，比起矩阵来具有节省存储空间和方便插值的优点。本文主要归纳了两种表达方式的转换，计算公式采用3D笛卡尔坐标系：

图1 3D Cartesian coordinate System (from wikipedia)

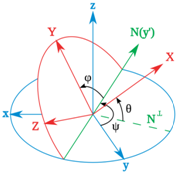
定义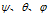分别为绕Z轴、Y轴、X轴的旋转角度，如果用Tait-Bryan angle表示，分别为Yaw、Pitch、Roll。

图2 Tait-Bryan angles (from wikipedia)

一、四元数的定义

通过旋转轴和绕该轴旋转的角度可以构造一个四元数：

其中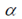是绕旋转轴旋转的角度，为旋转轴在x,y,z方向的分量（由此确定了旋转轴）。

二、欧拉角到四元数的转换

三、四元数到欧拉角的转换

       arctan和arcsin的结果是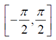，这并不能覆盖所有朝向(对于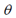角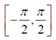的取值范围已经满足)，因此需要用atan2来代替arctan。

四、在其他坐标系下使用

在其他坐标系下，需根据坐标轴的定义，调整一下以上公式。如在Direct3D中，笛卡尔坐标系的X轴变为Z轴，Y轴变为X轴，Z轴变为Y轴（无需考虑方向）。

五、示例代码

http://www.cppblog.com/Files/heath/Euler2Quaternion.rar
Demo渲染两个模型，左边使用欧拉角，右边使用四元数，方向键Up、Left、Right旋转模型。

参考文献：

[1] http://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles

[2] Ken Shoemake, Animating Rotation with Quaternion Curves, 1985

转载请注明：徐自远的乱七八糟小站 » 【原创】F303RE(NUCLEO)+MPU6050输出欧拉角