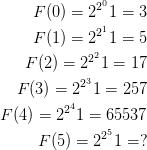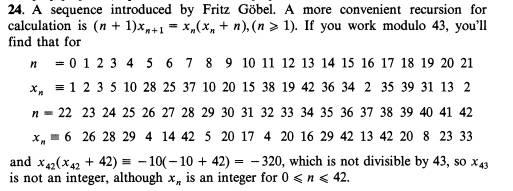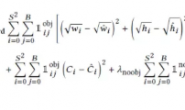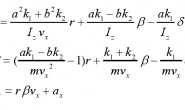【这些极有可能成立的数学猜想,却都存在一个大反例!】

只差一步
就成为了定理
上期回顾:五大蒙蔽你的数学假象(传送门),今天继续!
1
The Strong Law ofSmall Numbers 论文中提到的一些例子节选
论文其实就是要表明一个观点:You cannot tell by looking.
A.费马数:
若为素数,其必要条件是
为2的幂
证:
假设有某个奇数因子
,设
,k为正整数
为不为1的正整数
所以含因子
,为合数,矛盾!
那么反过来是不是每一个2的幂对应一个素数呢,著名民间科学家费马发现
(求教Latex怎么左对齐……)
前5个是质数,因为第6个数实在太大了,费马认为是质数。
1640年费马猜想:的数都是质数
(费马没给出证明……)
反例:
1732年擅长计算的Euler给出
注:
之后人们利用计算机一口气算到了n=46以后,发现n大于4小于47时,Fn都是合数
目前只知道n=0,1,2,3,4时,F(n)是素数
甚至有人猜想,n>4时,F(n)均是合数…(还没有反例)
费马如果能看到,他的表情一定是:
B.梅森素数
如果是素数,那么一个必要条件是n是素数,证明和A相似,这里略去
但是若n是素数,一定是素数么?
计算一下,当n=2,3,5,7时是对的
反例:
注:本来并不想写出这个梅森素数,因为这个反例并不巨大,但是其很著名,同时也反映了一些问题。
寻找梅森素数一直是一个有趣的课题,是否存在无穷多个梅森素数仍然是数论中未解决的著名难题之一。
C.
D.
考虑数列
可以求出
猜想:总是一个整数
事实上,这对n<30均成立
反例:
不是整数。
证明如下:
得到递推式后,两边同时模43,如果是整数,那么两边会不同余
对于更多数列和素数上的巧合那就数不胜数了,可参见论文中更多例子
可见猜想虽然很多时候从直觉出发,但是因为从有限枚举的情况不能推出无穷种情况都成立,然而人类处理的数字公式和数列越来越多的时候,那么就会自然而然出现巧合了,
因为只有1个1,1个2,1个3,1个4,1个5,1个6,1个7,……却有无穷个数列和无穷多个数学问题,所以各种巧合很有可能发生,但是由于计算能力有限我们往往枚举过程中探知不到矛盾。
E.
对n为正整数总是互素么?
如果用计算机去从1开始一个个验证,那么计算机是无法发现反例的
(很有可能运行超时)
其实对于1亿亿内的n都可以成立这个命题
但是这真的对所有n成立麽?
反例:
第一个出现在
2
佩尔方程
很多时候知道一些数学知识后,才能轻易地解决一些看似很复杂的东西。
假定你不知道佩尔方程的理论,那么关于方程
的正整数解的存在性,
来试图得到一些解,可是无功而返。
由于,也许x会比较大吧,我们可以通过程序来跑一跑
x,y在1~10000之间时是否能够得到解
(省略程序)
然而还是无功而返。
如果我告诉你,在x或y小于一万亿的范围内方程还是没有正整数解!
你是否会
猜想:
方程没有正整数解
反例:
且这是方程最小正整数解
注:
好了……这个正整数解肯定不是靠遍历跑出来的,计算机也吃不消
是连分数序列的最小正周期,
若是偶数,则就是方程的一组特解,
否则是方程的一组特解。
证明参考任何一本讲述了Pell方程的初等数论书籍或者wiki
Pell方程即形如的方程,D是正整数但不是完全平方数
事实上我们可以证明,Pell方程一定有无穷多组正整数解,这是初等数论一个经典结果。
可见:
很多时候一些对小数验证的猜想不一定对大数成立。
这就是为什么很多关于否定方程的正整数解的命题(如费马大定理)不能通过验证较小的整数达到证明目的(如1万亿以内),比如这个Pell方程,其在x,y小于一万亿的范围内也是没有解的,但是它有解而且有无穷多正整数解。
这恰好说明了发展数学理论的重要性,比如Pell方程其理论与连分数算法都是经过研究得到的(Lagrange有重要贡献),而不是单纯的枚举法。
再注:
阿基米德群牛问题
论阿基米德为什么要带那么多牛来到西西里岛……
3
不知道具体数字的反例
数论中一个非常漂亮的结果就是素数定理:
即对正实数,定义
为不大于的素数个数,我们可以用一些初等函数来估计π(x),从而较对素数分布得到一些较精确的结果
一个直观的理解就是当N充分大时,在1到N之间任取一个数,其是素数的概率大概为
这个结果等价于时
其中
(不难证明积分存在且有限)
第二个等价成立的原因可以用洛必达法则证明
问题来了:
既然,那么究竟有多接近呢?
下面有一组数据
第一列为n的值,第二列为的值,第三列为
的值(取6位有效数字)
似乎总有第二列对应值<第三列对应值
猜想:
这个猜想确实是Reasonable的,上面写的那些等价无穷大的结论都是对的。
并且我们有了很多类似的结果如
(当x大于55)
(当x大于355991)
哪怕我们能找到一个确定的N,使n>N时有
我们就可以对n在1-N之间有限的情况验证即可
(这种技巧在数论证明中真是屡见不鲜,有限情况都靠计算机即可)
反例:
John Edensor Littlewood 1914年证明了这样的n一定存在
使得
All numerical evidence then available seemed to suggest that π(x) was always less than li(x). Littlewood’s proof did not, however, exhibit a concrete such numberx
他还进一步证明了在会无穷多次变号
注:
接下来该我们的Stanley Skewes 出场了
Stanley Skewes 何许人也?
南非数学家,Littlewood 的学生之一,Littlewood是他的研究生导师,肯定当时给了他这个题目让他做……
Stanley Skewes于1933年证明了存在一个自然数n,n小于使得
不过他用到了黎曼猜想是正确的这个假设
当年他34岁……
Stanley Skewes于1955年证明了存在一个自然数n,n小于使得
不过这次他摆脱了黎曼猜想是正确的这个假设,可谓真正的证明了上界的存在性。
当年他56岁…
现在,我们用Skewes’ number表示最小的自然数n使得
现在有更好的估计 Skewes’ number比小
但是可见它还是很大,所以计算机不能很好地计算出它(计算能力还是不够……)
但是它还是很小的,如果和葛立恒数相比,它远远小于葛立恒数
转载请注明:徐自远的乱七八糟小站 » 【这些极有可能成立的数学猜想,却都存在一个大反例!】