FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在圈圈就根据实际经验来说说FFT结果的具体物理意义。一个模拟信号,经过ADC采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。而每个点的相位呢,就是在该频率下的信号的相位。第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。例如某点n所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn所能分辨到频率为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号a*a+b*b,相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号,是直流分量,幅度即为A1/N。
由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
< 现在进入Excel 应用部分>
| Time |
A |
nA |
| 23:55:43 |
0.000050533 |
50.53 |
| 23:55:43 |
0.000050596 |
50.60 |
| 23:55:43 |
0.000050701 |
50.70 |
| 23:55:44 |
0.000050723 |
50.72 |
| 23:55:44 |
0.000050775 |
50.78 |
| 23:55:44 |
0.000050407 |
50.41 |
| 23:55:44 |
0.000050554 |
50.55 |
| 23:55:44 |
0.000050638 |
50.64 |
| 23:55:45 |
0.000050670 |
50.67 |
| 23:55:45 |
0.000050375 |
50.38 |
| 23:55:45 |
0.000050575 |
50.58 |
| 23:55:45 |
0.000050628 |
50.63 |
| 23:55:45 |
0.000050786 |
50.79 |
| 23:55:46 |
0.000050754 |
50.75 |
| 23:55:46 |
0.000050691 |
50.69 |
数据源格式如上。列A 采样时间, 列B 是收集结果。列C 把B 的结果放大100万倍。
1) Excel中, 数据 -> 数据分析 -> 选中傅立叶计算包;
2)输入区域中: C2:C1025 ( 取 1024个样本)
3)点确定输出。
输出效果如下:
| -1.5761686655323-13.154170211423i |
13.24826 |
| 7.51527679786072-12.3462378230758i |
14.45368 |
| 4.1040242459709-12.9985667365274i |
13.63106 |
| 0.753456344407055-7.14076561808764i |
7.180406 |
| 2.41774879336855-12.4363683220093i |
12.66921 |
| 0.979004203596167-7.34345190071712i |
7.408423 |
| 1.0364171188506-12.3564407529179i |
12.39983 |
| 0.966937618659785-11.5644619240511i |
11.60482 |
| 3.80598075250153-9.41303134539053i |
10.15336 |
列A 是计算结果, 列B 对列A 取模, Excel 函数 IMABS()
对列B做折线图:
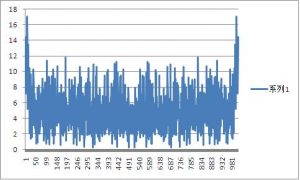
可以观察到,即使去除两边的超显性量,对观察频率没有任何帮助。
我们把样本减少一半,取样 512 个, 结果如下:
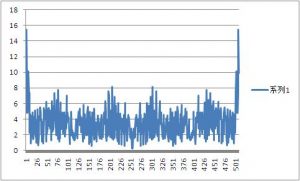
这样可以观察到可读的形状了。
现在计算周期:
对应频率 = 样本点 × 取样频率 / 总样本数
那么第 76 个点对应的频率 大约 0.75Hz
转载请注明:徐自远的乱七八糟小站 » 尝试用Excel 完成 FFT 分析




