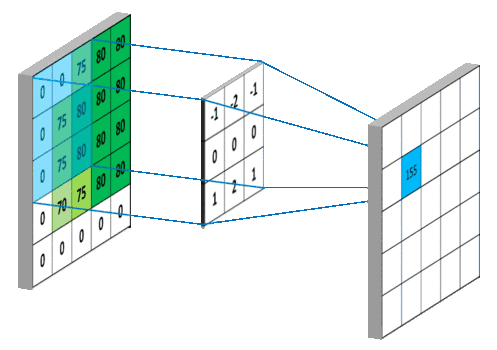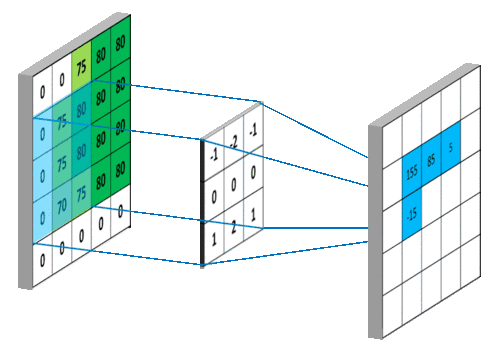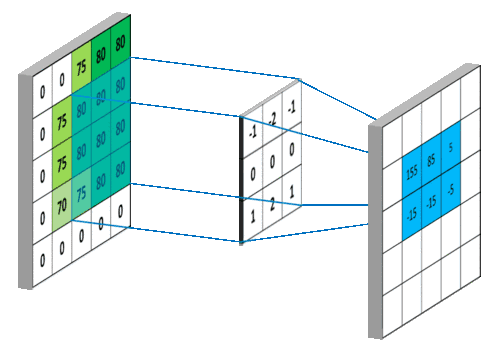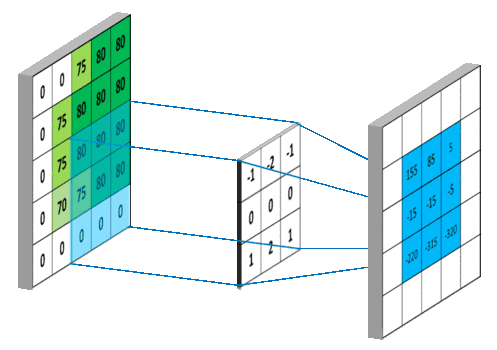
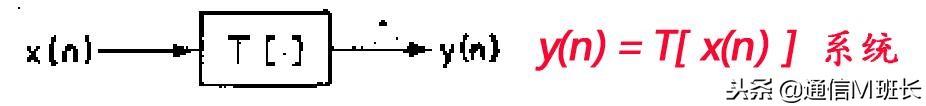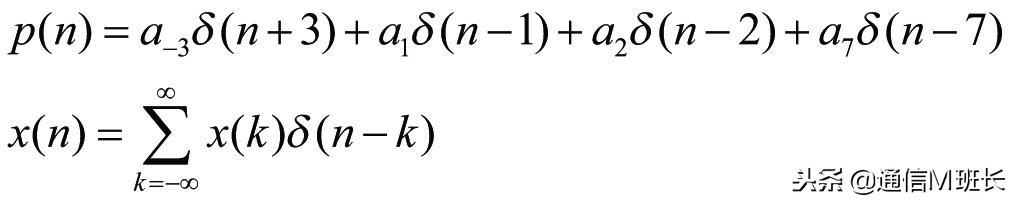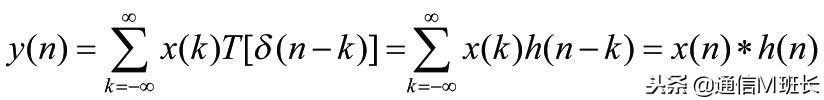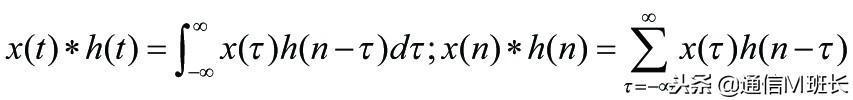卷积:翻转后的乘加运算,更是一种三维运算;不一样的卷积理解
【通信技术基础第11讲】
卷积是一种运算,就像加法、乘法一样。它的特别之处在哪里?
系统中的卷积
对于一个离散系统T而言,输入信号为δ(n),输出信号为h(n),h(n)称之为冲激响应;输入信号为x(n),输出信号为y(n)。
通过对单位冲激序列移位以及幅度加权,可以得到任意序列x(n)。按此方法可以得出图3序列的表达
使用冲激序列δ(n)表达p(n)
根据x(n)的冲激序列表达式,我们可以推导y(n).由于我们通常研究线性时不变系统,所谓时不变就是,当系统输入δ(n)时,输出为h(n);当系统输入δ(n-k)时,系统输出h(n-k)。所以:
OK,为了简化系统输出表达式,我们把这种运算定义为卷积,即系统输出响应y(n)就是输入x(n)与冲激响应h(n)的卷积,*是卷积运算符号。
卷积的定义
连续时间系统x(t)与h(t),离散时间序列x(n)与h(n),卷积的定义:
有一个特点,就是 τ+(n-τ)=n,如果令x= τ,y=n-τ,x+y=n,画在坐标轴上就像这样:
如果遍历这些直线,就好比,把毛巾沿着角卷起来。感谢知乎马同学给出这样一种直观理解卷积的方法。没错,卷积就如同卷起毛巾一样,移动一步,翻转一步,乘加一步!
卷积的计算
顾名思义,卷积就是卷起来,褶起来求积。所以卷积也叫做褶积。具体的步骤如下图所示,这也是最经典的卷积求法,画图法,直观上更好理解。
现在我们可以使用matlab中的卷积函数cov辅助我们快速的求得卷积结果。但经典画图法还是推挤大家一试,在画图的过程中,可以体会到“卷”的含义!
在时间轴上横向移动,然后以纵轴进行翻转,所以我把它叫做一种“三维”的运算方式。
图像处理中,二维卷积使用的次数更为频繁,这里不再详细介绍。
卷积:翻转后的乘加运算,更是一种三维运算;不一样的卷积理解http://t.jinritoutiao.js.cn/8oK7pa/