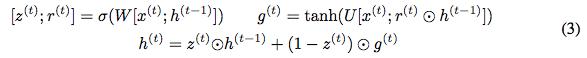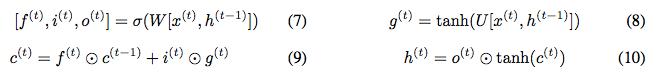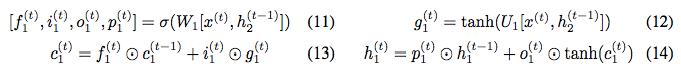作者:Matthew MacKay等
机器之心编译
参与:高璇、张倩
循环神经网络(RNN)在处理序列数据方面取得了当前最佳的性能表现,但训练时需要大量内存。可逆循环神经网络提供了一个减少训练内存需求的路径,因为隐藏状态不需要存储,而是可以在反向传播过程中重新计算。本文首先展示了不需要存储隐藏激活的完全可逆 RNN 从根本上是有限制的,因为它们不能忘记隐藏状态的信息。然后,研究人员提供了一个存储少量比特的方案,使遗忘信息实现完全逆转。本文的方法实现了与传统模型相当的性能,但所需内存只占传统模型的 1/10 到 1/15。
循环神经网络(RNN)在语音识别 [1]、语言建模 [2,3] 和机器翻译 [4,5] 等多种任务上都取得了极优的性能。然而,训练 RNN 需要大量的内存。标准的训练算法是时间截断的反向传播(TBPTT)[6,7]。该算法将输入序列划分为较短的子序列 T,然后对每个子序列进行处理,并对梯度进行反向传播。如果模型隐藏状态的大小为 H,那么 TBPTT 所需的内存是 O(T H)。
减少 TBPTT 算法对内存的需求会增加被截断序列的长度 T,从而抓取更长的时间尺度上的相关性。也可以增加隐藏状态的大小 H,或者利用更深层的输入到隐藏、隐藏到隐藏或隐藏到输出转换,从而赋予模型更强的表达能力。增加这些转换的深度可以提高复调音乐预测、语言建模和神经机器翻译(NMT)的性能 [8,9,10]。
可逆循环网络架构提供了一种降低 TBPTT 内存需求的方法。可逆架构实现了在给定下一个隐藏状态和当前输入的当前时间步上的隐藏状态重建,这样无需在每个时间步上存储隐藏状态就能执行 TBPTT。代价就是要增加计算成本来重建反向传播过程中的隐藏状态。
本文首先介绍了广泛使用的门控循环单元(GRU)[11] 和长短期记忆(LSTM)[12] 架构的可逆相似架构。然后证明,任何不需要存储隐藏激活的完全可逆的 RNN,在一个简单的一步预测任务中都会失败。即使这个任务对于普通的 RNN 很简单,但在完全可逆模型中却失败了,因为它们需要记住输入序列才能完成任务。根据这一发现,研究人员扩展了 Maclaurin 等人 [13] 的高效内存反转法,在每个单元中存储少量的比特,以对遗忘信息的架构进行完全逆转。
研究人员在语言建模和神经机器翻译基准上评估了这些模型的性能。根据任务、数据集和所选架构,可逆模型(无注意力机制)所需内存只占传统模型的 1/10 到 1/15。可逆模型在 Penn TreeBank 数据集 [14] 上的词级语言建模任务中得到了与传统的 LSTM 模型和 GRU 模型相似的性能,在 WikiText-2 数据集 [15] 上比传统模型困惑度落后 2-5 个点。
使用基于注意力的循环序列到序列模型来节省内存是很困难的,因为为执行注意力机制,编码器的隐藏状态必须同时保存在内存中。对与嵌入词相连的隐藏状态的子集执行注意力机制,可以解决这一问题。使用这种技术后,可逆模型在神经机器翻译任务中取得了成功,在 Multi30K 数据集 [16] 上的性能优于基线 GRU 和 LSTM 模型,并在 IWSLT 2016[17] 基准上取得了很有竞争力的表现。使用该技术可以将内存在解码器中减少到原来的 1/10-1/15,在编码器中减少到原来的 1/5-1/10。
论文:Reversible Recurrent Neural Networks
论文链接:https://arxiv.org/pdf/1810.10999v1.pdf
摘要:循环神经网络(RNN)在处理序列数据方面取得了当前最佳的性能表现,但训练时需要大量的内存,限制了可训练的 RNN 模型的灵活性。可逆的 RNN-RNN 可以对其进行隐藏状态到隐藏状态的转换,提供了一个减少训练内存需求的路径,因为隐藏状态不需要存储,而是可以在反向传播过程中重新计算。我们首先展示了不需要存储隐藏激活的完全可逆 RNN,从根本上是有限制的,因为它们不能忘记隐藏状态的信息。然后,我们提供了一个存储少量比特的方案,使遗忘信息实现完全逆转。我们的方法实现了与传统模型相当的性能,同时激活内存开销变为原来的 1/10-1/15。然后我们将技术扩展到基于注意力的序列到序列模型,在这种模型中性能不变,但将内存开销在解码器中减少到原来的 1/10-1/15,在编码器中减少到原来的 1/5-1/10。
3 可逆循环架构
构建 RevNet 的技术可以与传统的 RNN 模型相结合,生成可逆的 RNN。在本节中,我们提出了类似 GRU 和 LSTM 的可逆架构。
3.1 可逆 GRU
我们首先回顾一下,在给定当前隐藏状态 h^(t) 和当前输入 x^(t)(省略偏差)时计算下一个隐藏状态 h^(t+1) 的 GRU 方程:
方程中的⊙表示元素的乘法。为了使更新可逆,我们将隐藏状态 h 分成两组,h = [h_1; h_2]。使用以下规则更新这些组:
注意,h_1^(t) 和非 h_1^(t-1) 用于计算 h_2^(t) 的更新。我们把这个模型称为可逆门控循环单元或 RevGRU。
3.2 可逆 LSTM
接下来构造一个可逆的 LSTM。该 LSTM 将隐藏状态分为输出状态 h 和单元状态 c,更新方程为:
我们不能直接使用我们的可逆方法,因为 h^(t) 的更新不是 h^(t-1) 的非零线性变换。尽管如此,可通过使用如下方程来实现可逆:
我们使用 c_1^(t) 和 h_1^(t),利用与上述等式相同的方式计算 c_2、h_2 的更新。我们将此模型称为可逆 LSTM 或 RevLSTM。
3.3 有限精度算法的可逆性
我们已经定义了在精准算法中可逆的 RNN。但在实际中,由于数值精度有限,隐藏状态不能被完全地重建。考虑 RevGRU 方程 4 和 5,如果隐藏状态 h 存储在固定点中,则将 h 乘以 z(其条目小于 1)会破坏信息,从而阻止完全重建。例如,将隐藏单位乘以 1/2 相当于丢弃最低位字节,其值在反向计算中无法恢复。信息丢失的这些误差在时间步长上呈指数级累积,导致通过反转获得的初始隐藏状态与真实的初始状态相去甚远。同样的问题也会影响 RevLSTM 隐藏状态的重建。因此,我们发现遗忘是构建完全可逆的循环架构的主要障碍。
解决这一问题有两种可行途径。首先是移除遗忘步骤。对于 RevGRU,这意味着我们像以前一样计算 z_i^(t) 、 r_i^(t) 和 g_i^(t),并使用以下方法更新 h_i^(t):
我们将此模型称为无遗忘(No-Forgetting)RevGRU 或 NF-RevGRU。因为 NFRevGRU 的更新不会丢弃信息,所以在给定时间内的训练过程中,我们只需要在内存中存储一个隐藏状态即可。可以采用类似的步骤定义 NF-RevLSTM。
第二种方法是接受一些内存使用,并将从隐藏状态中遗忘的信息存储在前向传播中。然后,我们可以在反向计算中将这些信息还原到隐藏状态,以实现完全重建。具体内容将在第 5 节中详细讨论。
4 No Forgetting 的不可能性
我们已经证明,如果不丢弃任何信息,可以构造出具有有限精度的可逆 RNN。我们无法找到能够在语言建模之类的任务上获得理想性能的架构。这与之前发现的遗忘对 LSTM 性能至关重要是一致的 [23,24]。在本节中,我们认为这是由不可遗忘可逆模型的一个基本限制造成的:如果任何隐藏状态都不能被遗忘,那么任何给定时间步上的隐藏状态必须包含足够的信息,来重建所有以前的隐藏状态。因此,在一个时间步长上存储在隐藏状态中的任何信息都必须保留在将来的所有时间步上,以确保精准重构,这超过了模型的存储容量。
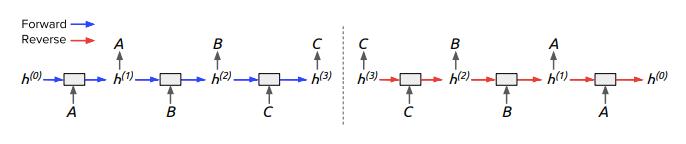
图 1:在重复任务上展开完全可逆模型的反向计算,得到序列到序列的计算。左:重复任务本身,模型重复每个输入指令。右:展开反转。模型有效利用最终隐藏状态来重构所有输入指令,这意味着整个输入序列必须存储在最终隐藏状态中。
5 遗忘的可逆性
由于零遗忘不可能实现,我们不得不探索实现可逆性的第二种方案:在前向计算中存储隐藏状态丢失的信息,在反向计算中恢复信息。最开始我们研究了只允许遗忘一个整数位的离散遗忘。这导致:如果前向传递中遗忘了 n 位字节,我们可以将这 n 位字节存储在堆栈中,在重构期间弹出并恢复到隐藏状态。但是,与基线模型相比,限制我们的模型仅仅遗忘整数位字节就会导致性能大幅下降。本文接下来的内容会侧重只遗忘一小部分字节的部分遗忘。
5.2 注意力机制下的内存节省
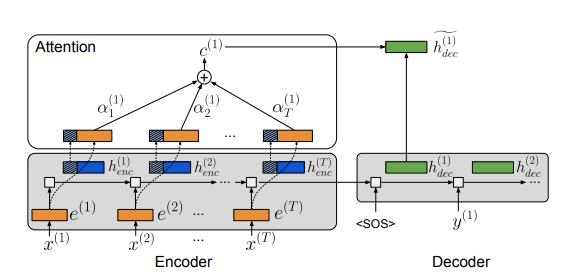
图 2:NMT 的注意力机制。词嵌入、编码器隐藏状态和解码器隐藏状态分别用橙色、蓝色和绿色表示;编码器隐藏状态的条纹区域表示为注意力机制而存储在内存中的部分。用于计算上下文向量的最后几个向量连接了词嵌入和编码器隐藏状态。
6 实验
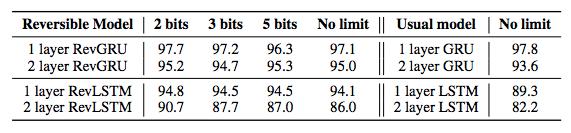
表 1:Penn TreeBank 词级语言建模上的验证困惑度(内存节省)。在没有限制的情况下,当遗忘被限制在 2 位、3 位和 5 位比特时,每个隐藏单元每个时间步的结果显示如表。
表 2: WikiText-2 词级语言建模上的验证困惑度。在没有限制的情况下,当遗忘被限制在 2 位、3 位和 5 位比特时,每个隐藏单元每个时间步的结果显示如表。
表 3:不同的遗忘限制下 Multi30K 数据集的性能。P 为测试 BLEU 分数;M 表示编码器在训练期间平均节省的内存。
本文为机器之心编译,转载请联系本公众号获得授权。