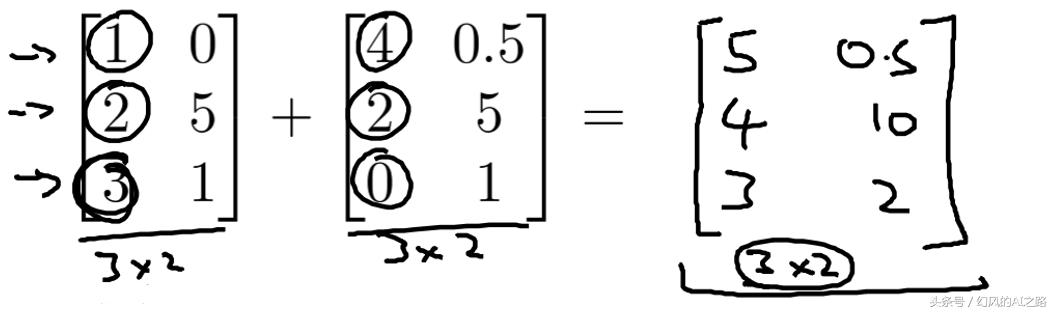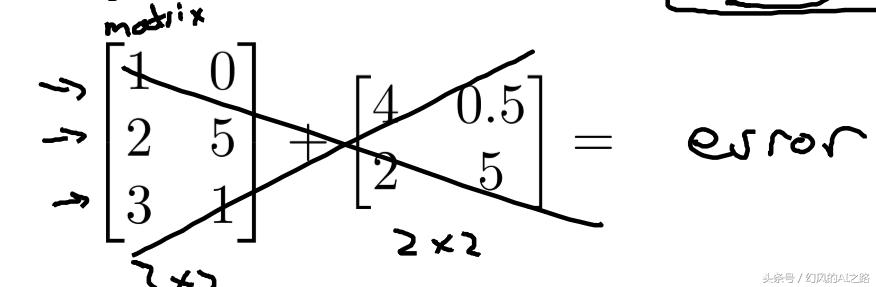本文重点：吴恩达老师再第三章课程中补充了一些线性代数的知识，一共有6节课程，主要介绍数学知识，但是内容不多，所以这篇文章是全部第三章的内容。

3 – 1 – Matrices and Vectors

矩阵和向量

矩阵：由数字组成的矩形数列，并写在括号中间：

其实我们可以说矩阵是二维数组的另外一个名字。

矩阵的维度=矩阵的行数*矩阵的列数

上面的矩阵是4*2维

指第行，第列的元素。

向量是一种特殊的矩阵，所以向量也可以理解维矩阵，它是n*1列，向量在吴恩达老师的课程中一般指的是列向量，比如：

y为四维列向量（4×1），yi表示向量中的第几个元素。

下图为 1 索引向量和 0 索引向量，左图为 1 索引向量，右图为 0 索引向量，一般我们用 1 索引向量。

我们用大写字母表示矩阵，小写字母表示向量

3 – 2 – Addition and Scalar Multiplication (7 min).

加法和标量乘法

行数和列数相等矩阵可以相加，就是对应位置相加

如果行数和列数不相等是无法相加的：

矩阵的标量乘法：每个元素都要乘

3 – 3 – Matrix Vector Multiplication

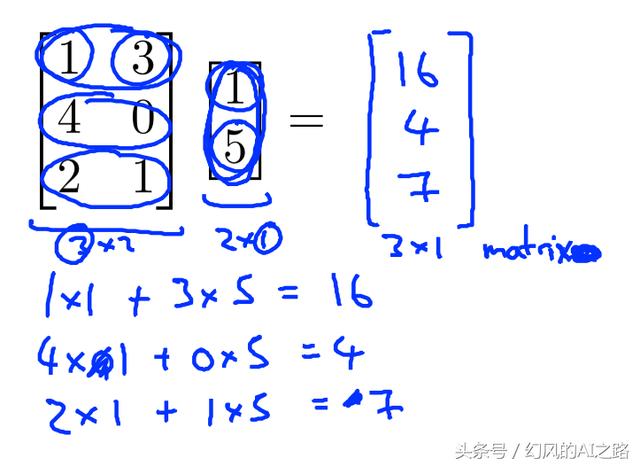
矩阵和向量乘法

× 的矩阵乘以 × 1的向量，得到的是 × 1的向量

3 – 4 – Matrix Matrix Multiplication (11 min).mkv

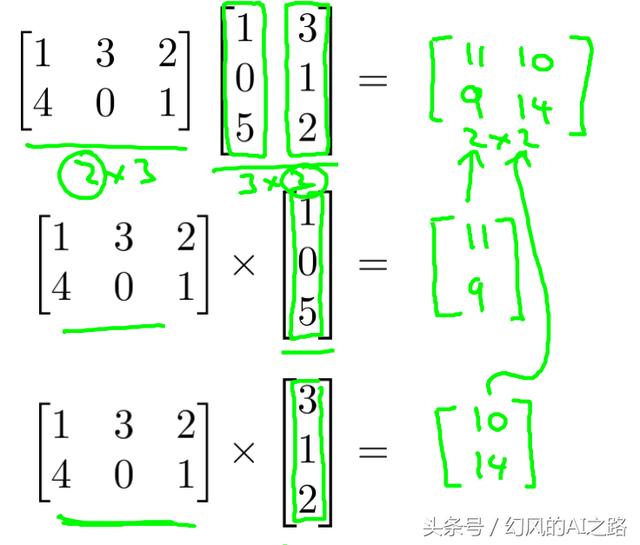
矩阵和矩阵的乘法

× 矩阵乘以 × 矩阵，变成 × 矩阵

3 – 5 – Matrix Multiplication Properties (9 min)

矩阵乘法的本质

矩阵的乘法不满足交换律： × ≠ ×

矩阵的乘法满足结合律即： × ( × ) = ( × ) ×

单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1,我们称

这种矩阵为单位矩阵．它是个方阵，一般用 或者 表示，本课程都用代表单位矩阵，

从左上角到右下角的对角线（称为主对角线）上的元素均为1以外全都为0。如：

−1 = −1 = （−1是A的逆矩阵，因为头条不好表示数学符号的原因