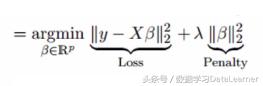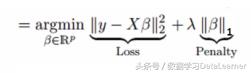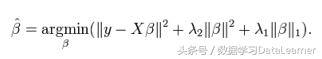本文来自AnalyticsVidhya的一个分析。线性回归和逻辑回归通常是人们在预测建模中学习的第一个算法。由于受欢迎程度，许多分析师甚至认为他们是唯一的回归形式。更多的人认为他们是所有形式的回归分析中最重要的。

事实是，有无数形式的回归方法。每种形式都有其自身的重要性和最适合应用的特定条件。本文将以简单的方式解释了最常用的7种形式的回归方法。通过这篇文章，希望人们能够形成回归广度的概念，而不是仅仅对他们遇到的每个问题应用线性/逻辑回归，并希望它们能够适合！

1、什么是回归分析

回归分析是预测建模技术的一种形式，它研究因变量（目标）和自变量（预测变量）之间的关系。 该技术用于预测、时间序列建模、查找变量之间的因果关系等。例如，通过回归可以研究疲劳驾驶与道路交通事故数量之间的关系。

回归分析是建模和分析数据的重要工具。 在这里，我们将曲线/线拟合到数据点，使得数据点距曲线或线的距离之间的差异最小化。

2、为什么要使用回归分析

如上所述，回归分析估计两个或更多变量之间的关系。 让我们通过一个简单的例子理解这一点：

比方说，您想根据当前的经济状况估算公司的销售增长率。 您有最近的公司数据表明销售增长约为经济增长的2.5倍。 利用这种洞察力，我们可以根据当前和过去的信息预测公司的未来销售情况。

使用回归分析有很多好处：

1. 首先，它可以表明因变量和自变量之间的重要关系。
2. 其次，它还表示多个自变量对因变量的影响强度。

回归分析还允许我们比较在不同尺度上变量的影响，例如价格变化和促销活动的数量的影响。这些优势有助于市场研究人员/数据分析师/数据科学家消除和评估用于构建预测模型的最佳变量集。

3、有多少种回归方法

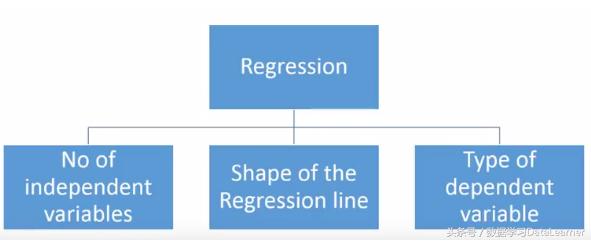
有各种各样的回归技术可用于进行预测。 这些技术主要由三个指标（自变量的数量，因变量的类型和回归线的形状）驱动。 我们将在以下部分详细讨论它们。

3.1、线性回归（Linear Regression）

它是最广为人知的建模技术之一。 线性回归通常是人们在学习预测建模时优先选择的技术之一。在该技术中，因变量是连续的，自变量可以是连续的或离散的，并且回归线的性质是线性的。

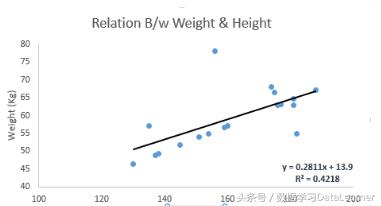
线性回归使用最佳拟合直线（也称为回归线）在因变量（Y）和一个或多个自变量（X）之间建立关系。

它由等式Y = a + b * X + e表示，其中a是截距，b是线的斜率，e是误差项。该等式可用于基于给定的变量预测结果。

简单线性回归和多元线性回归之间的区别在于，多元线性回归具有一个以上的独立变量，而简单线性回归只有1个独立变量。

3.2、逻辑回归（Logistic Regression）

Logistic回归Y的值的范围从0或者1。就不赘述了。

3.3、多项式回归（Polynomial Regression）

如果自变量的最高次大于1，那么就是多项式分布：

y = a + bx^2

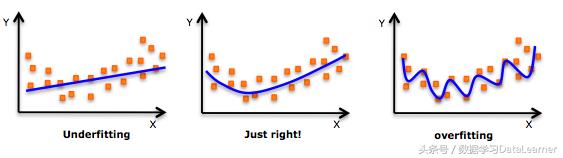
​多项式回归拟合的是一条曲线，不是直线。注意最高次越大拟合能力越强，但也容易造成过拟合。

3.4、逐步回归（Stepwise Regression）

当我们处理多个自变量时，会使用这种形式的回归。 在这种技术中，自变量的选择是在自动过程的帮助下完成的，该过程不涉及人为干预。

这是通过观察R-square，t-stats和AIC metric等统计值来识别重要变量来实现的。逐步回归根据某个指定的标准，在每次训练的时候增加或者减掉一个协方差变量来适配模型。

标准逐步回归做两件事。它根据每个步骤的需要添加和删除预测变量。正向选择从模型中最重要的预测变量开始，并为每个步骤添加变量。向后消除从模型中的所有预测变量开始，并删除每个步骤的最不重要变量。

该建模技术的目的是以最少的预测变量来最大化预测能力。 它是处理数据集更高维度的方法之一。

3.5、岭回归（Ridge Regression）

岭回归是当数据遭受多重共线性（独立变量高度相关）时使用的技术。在多重共线性中，即使最小二乘估计（OLS）是无偏的，它们的方差也很大，这使得结果远离真实值。通过向回归估计添加一定程度的偏差，岭回归可以减少标准误差。

例如线性回归的公式如下

y = a + b * x

添加一个误差项：

y = a + b * x + e

在线性方程中，预测误差可以分解为两个子分量。分别是偏差（bias）和方差（variance）。 由于这两个或两个组件中的任何一个，可能发生预测错误。 在这里，我们将讨论由于方差引起的错误。

岭回归通过收缩参数λ（lambda）解决了多重共线性问题:

在这个等式中，我们有两个组成部分。 第一个是最小二乘项，另一个是β2（β平方）总和的λ，其中β是系数。 这被添加到最小平方项，以便缩小参数使结果具有非常低的方差。详细的岭回归方法可以参考回归分析方法之岭回归（Ridge Regression）

该回归的假设与最小二乘回归相同，但不假设正态性。它会缩小系数的值，但不会达到零，这表明它没有特征选择功能。这是一种正则化方法并使用l2正则化。

3.6、Lasso Regression

与岭回归相似，Lasso（Least Absolute Shrinkage and Selection Operator，最小绝对收缩和选择算子）也会对回归系数的绝对大小进行惩罚。 此外，它还能够降低线性回归模型的可变性并提高其准确性。 请看下面的等式：

​​

Lasso回归与岭回归的不同之处在于它在惩罚函数中使用绝对值而不是二次方。这导致一些参数估计的结果为零。这导致可以对给定n个变量的进行变量选择。

• 该回归的假设与最小二乘回归相同，但不假设正态性
• 它将系数缩小到零（正好为零），这肯定有助于特征选择
• 这是一种正则化方法并使用l1正则化
• 如果预测变量组高度相关，则Lasso回归仅选择其中一个并将其他预测变为零

3.7、弹性网络回归（ElasticNet Regression）

ElasticNet是Lasso和Ridge Regression技术的混合体。它同时使用L1和L2进行训练。 当存在多个相关的特征时，弹性网络回归很有用。 Lasso很可能随机选择其中一种，而弹性网很可能同时选择其中之一。

​​

在Lasso和Ridge之间进行权衡的一个实际优势是，它允许Elastic-Net在旋转下继承Ridge的一些稳定性。

• 它可以在高度相关的变量的情况下鼓励群体效应
• 所选变量的数量没有限制
• 它会遭受双重收缩

4、如何选择哪种回归技术

当你只知道一两种技术时，生活通常很简单。 我所知道的其中一个培训机构告诉他们的学生 – 如果结果是连续的 – 应用线性回归。 如果是二进制 – 使用逻辑回归！ 但是，我们可以使用的选项数量越多，选择合适的选项就越困难。 回归模型也会发生类似的情况。

在多种类型的回归模型中，基于独立变量和因变量的类型，数据中的维数以及数据的其他基本特征来选择最适合的技术是很重要的。 以下是您应该选择正确的回归模型的关键因素：

• 数据探索是构建预测模型的必然部分。在选择正确的模型之前，应该是您的第一步，例如确定变量的关系和影响
• 为了比较不同模型的拟合优度，我们可以分析不同的指标，如参数的统计显着性，R平方，调整后的r平方，AIC，BIC和误差项。另一个是Mallow的Cp标准。这基本上通过将模型与所有可能的子模型（或仔细选择它们）进行比较来检查模型中的可能偏差。
• 交叉验证是评估用于预测的模型的最佳方式。在这里，您将数据集划分为两个组（训练和验证）。观察值和预测值之间的简单均方差可以为您提供预测准确度的度量。
• 如果您的数据集有多个混淆变量，则不应选择自动模型选择方法，因为您不希望同时将它们放在模型中。
• 这也取决于你的目标。与统计上著名的一些模型相比，可以发现功能较弱的模型易于实现。
• 回归正则化方法（Lasso，Ridge和ElasticNet）在数据集中变量之间具有高维度和多重共线性的情况下运行良好。