主成分分析法（principal component analysis，PCA）和奇异值分析法（singular value decomposition，SVD）都是数据降维常用的方法。一般数据降维用于输入数据的预处理阶段，降低数据的维度、除去数据中包含的噪声。

PCA和SVD均应用于数据降维过程，这是两者最大的联系。而两者最大的区别在于各自应用的理论基础和实现过程上的不同。PCA是保证映射后的方差最大（丢失的信息最少），而SVD是通过奇异值分解的数学理论实现降维。两者的实现过程叙述如下。

1、PCA的实现过程

给定样本数据D={x1,x2,…,xm}；低维空间维数d。

（1）求解待降维数据各个维度上的均值（或称为中心化）；

（2）计算数据的协方差矩阵；

（3）计算协方差矩阵的特征值和特征向量（称为特征值分解）；

（4）取最大的d个特征值所对应的特征向量v1,v2,…,vd构成投影矩阵V={v1,v2,…,vd}。

（5）降维后的数据D’=D*V。

2、SVD实现过程

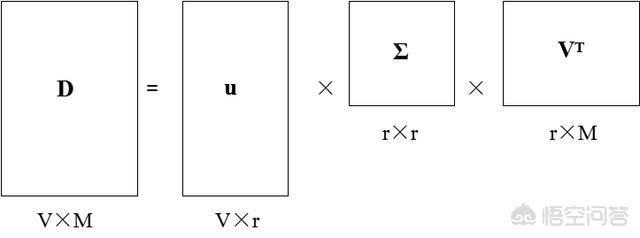
（1）对给定数据D进行奇异值分解，D=u*Σ*V^T（V^T为V的转置），如图所示，矩形下方标识的为矩阵的维数。

矩阵进行奇异值分解的数学基础较复杂，总的来说就是通过一系列的数学变换对矩阵实现上图所示的分解，而奇异值分解在程序上实现较为简便，用U,Sigma,VT=np.linalg.svd(Data)这一个语句（Python实现）就可实现数据的奇异值分解。

需要说明的是Σ矩阵是一个对角矩阵，，该矩阵的对角元素是从大到小排列的。这些对角元素称为奇异值。对应的就是原始数据集矩阵的奇异值。

(2)降维后的数据D’=D*V。

3、PCA和SVD在数学上的联系

PCA做的事情是对协方差矩阵对角化，即，而SVD是通过奇异值分解实现X=u*Σ*V^T。通过数学变换可以得到：

SVD中的矩阵u相当于PCA中的矩阵P，不过仅保留了的非零特征值对应的那些特征向量，而（也只保留了非零特征值）。SVD中的u代表了X中数据形成的正态分布的轴的方向（一组单位正交基），Σ/sqrt(n)代表了这些轴的长度（分布的标准差）。