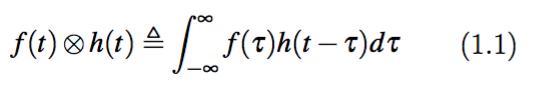卷积的定义

卷积实际上是两个信号的操作。

我们拿一维信号而言，两个一维时间信号的卷积f(t)*h(t)是这样定义的：

我们需要注意，两个一维时间信号的卷积f(t)*h(t)，结果仍然是一个关于时间t的函数。

这和我们在信号处理里面接触的很多变换不同，这些变换的结果，和原来的信号往往不在一个域。例如，一个时间函数f(t)的傅里叶变换F(ω)是频域信号。

卷积的数学意义

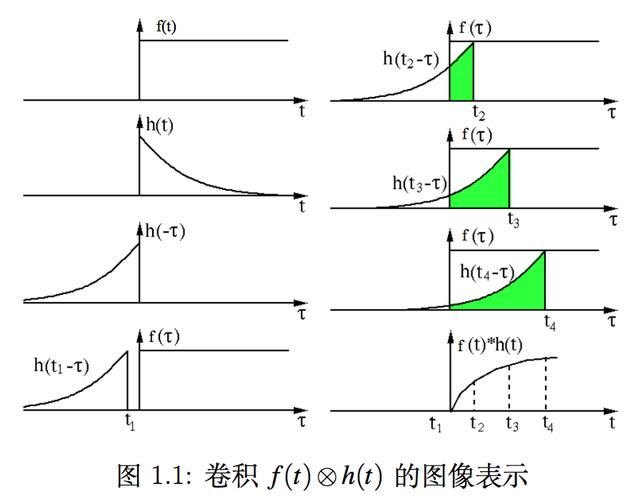
在卷积的定义式1.1中，等式右边的积分变量是τ。这样，h(t-τ)就是把h(τ)先按照纵轴对折，变成h(-τ)。

再将h(-τ)加一个时间上的偏移t。

然后把h(t-τ)同f(τ)相乘得到的函数在τ=[-∞,∞]覆盖的面积，就是得到了f(t)*h(t)。

注意，此时的这个面积，是对应某一个具体的t的时候卷积f(t)*h(t)的大小。

因为我们要得到所有的t时f(t)*h(t)的值，那么此时我们就需要去改变t。

对应的措施就是将t从-∞开始，沿着τ轴自左向右滑动。

每移动到一个新的位置t时，我们就计算这两个函数h(t-τ)和f(τ)的乘积函数的面积。这个面积就是卷积f(t)*h(t)在t处的值。

这个过程可以用图1.1来说明。

图示来解释卷积，其数学意义很清楚，但物理意义却模糊了。

为什么要把h(t)翻过来，为什么要做积分求面积？或者说到底，为什么我们需要卷积这么个奇怪的东西呢？

这个问题我们将在专栏的下一讲“什么是系统”中接着探讨。