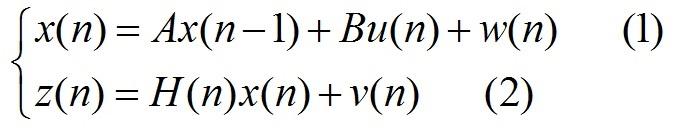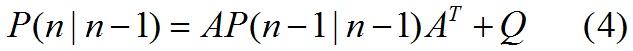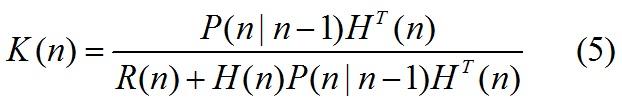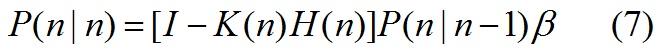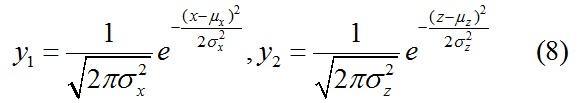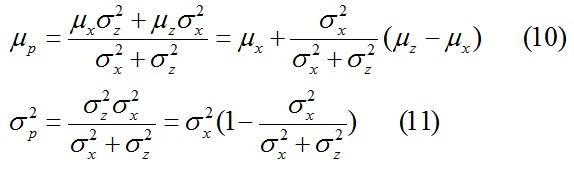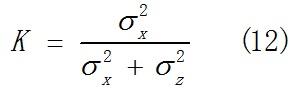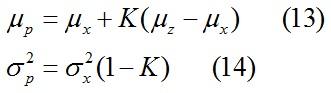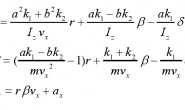卡尔曼滤波器是一种由卡尔曼(Kalman)提出的用于时变线性系统的递归滤波器。这个系统可用包含正交状态变量的微分方程模型来描述，这种滤波器是将过去的测量估计误差合并到新的测量误差中来估计将来的误差。

卡尔曼滤波器又是一个经常听到，但又从来都不了解的东东。为了了解他，我先找到了他的定义，卡尔曼滤波器在工业上应用广泛（没具体调查过。。。），而且结构简单（看了半天没看懂。。。）的一种数字线性滤波器。看到这里，我发现滤波器我知道是什么，但数字线性滤波器是什么呢，如果这都不知道，怎么学卡尔曼呢。于是，我就转战学习数字线性滤波器。在很久很久以后，我终于了解了什么是数字线性滤波器（数字其实换一种表达就是离散的，与其对应的就是连续。所谓线性呢，就是滤波器由线性方程（很重要的概念，以后有时间再说）表达）。看完了，我自信满满的去看卡尔曼滤波器，发现然并卵，依然神马都看不懂。无奈之下，只得硬着头皮一点一点的看公式，一点一点的理解，这才大概了解了什么是卡尔曼滤波器。这就说明了，遇到问题，必须迎面而上，绕是绕不过去的。本来可能一两天能看明白，由于畏难情绪，我花了一周多的时间去看数字线性滤波器，事倍功半啊。下面进入正题，到底什么是卡尔曼滤波器。

——————————————–分割线—————————————

在这里我要特别感谢xiahouzuoxin，看了他的博客之后，茅塞顿开。他举了生动的例子，进行详细的讲解，重要的是给出了对卡尔曼内涵的理解。本文只是在其基础上，多加了一些我自己不懂得解释。详细的例子可以去看大神博客，地址如下：

http://blog.csdn.net/xiahouzuoxin/article/details/39582483

——————————————–分割线—————————————

下面按照如下顺序介绍卡尔曼滤波器：

1.问题的提出：介绍卡尔曼滤波提出的原因以及针对的问题。

2.核心思想：一句话表述卡尔曼滤波本质。

3.应用场景：卡尔曼滤波器应用方向、基础和前提。

4.实现方法：经典的五个公式（配注释哦）。

5.定性分析：从单变量入手分析卡尔曼滤波器，定性的了解核心思想（非常直观哦！）。

——————————————–分割线—————————————

1.解决问题

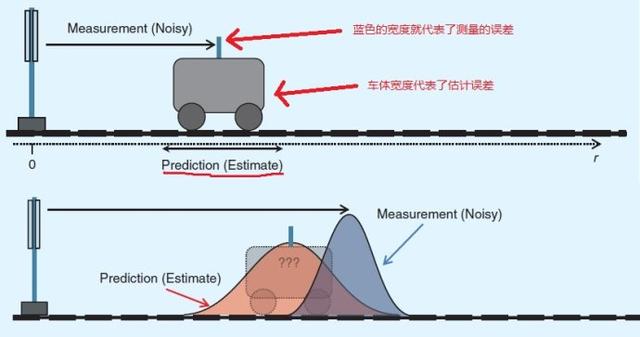
在对一个问题的线性估计（预测）中，估计（预测）出的结果会存在一定噪声（是个值得思考的问题），那么如何消除这个噪声呢？（可以看出，卡尔曼是为了消除噪声，这就是叫滤波器的原因吧。）那么很自然的我们可以想到用观测（直接测量估计量）来消除误差。但是，很不幸的是，观测的数据也会存在噪声（任何的测量都有误差）。下面问题归结表述为，已知估计值和测量值，以及估计和测量的误差，那么如何得到较为真实的数值？借用xiahouzuoxin的图，可以更加直观的看到估计和测量噪声存在的原因。

注：线性估计，就是根据当前状态和已有知识，推算出未来状态。举个例来说，已知当前小车速度和加速度，求取下一时刻速度。

2.核心思想

假设测量和估计的噪声都是符合高斯分布的白噪声。那么一个可行的办法是，将两个噪声的概率密度相乘，得到一个新的概率密度来近似表达真值。

注：两个高斯分布概率密度相乘后还是高斯分布。至于为什么是两个概率密度相乘，我理解是一个类似于求质心的感觉。

3.应用场景

3.1.观测系统以及估计系统均为线性离散系统，公式表述如下：

注：(1)式中x(n)为系统状态向量，u(n)是驱动输入向量，w(n)为估计噪声，A，B为常系数矩阵，其实就是状态空间中的状态方程。(2)式中z(n)为观测（测量）结果，H(n)为观测矢量，v(n)为观测噪声。

3.2估计噪声和观测噪声均为符合高斯分布的白噪声。所谓的白噪声就是时域上分布为钟形线，频域上分布为一条直线的噪声信号。

3.3两个符合高斯分布的概率密度相乘后可以融合为一个新的高斯分布。这一点也就是卡尔曼滤波方法的核心，具体推导过程将在第5部分给出。建议大家可以先自己推导一遍，这将对下面内容的理解非常有帮助。

3.4总结一下卡尔曼滤波器的应用场景。在测量和观测系统都为线性离散系统，同时两个的系统参数已知，而且噪声为符合高斯分布的白噪声的情况下，可以利用卡尔曼滤波器对信号进行滤波处理。

4.实现方法

下面给出卡尔曼滤波器经典的五个方程(我第一次看的时候也直接晕菜了，慢慢看其实很简单，如果看不懂先去看第5部分哦)，特别需要注意的是x(n|n)和x(n|n-1)是不一样的，可以将x(n|n-1)看作估计值（中间变量），x(n|n)才是当前最优估计值（结果）。同样，P(n|n)和P(n|n-1)也是这样的。此外，设估计噪声w(n)~N(0,Q)，测量噪声v(n)~N(o,R)。

4.1估计

由状态方程得到估计值，也就是x和P的中间值。

4.1.1状态估计

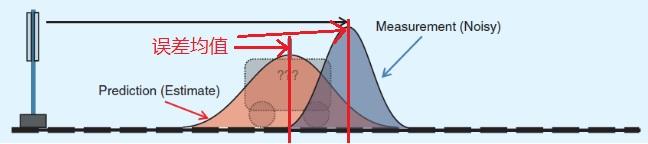
注：x(n-1|n-1)为上一时刻的最佳估计值。借用xiahouzuoxin的一张图，可以看出来其实估计值就是该时刻噪声的均值。

4.1.2最小均方误差矩阵

注：(1)最小均方误差矩阵可以理解为一维噪声方差的多维推广（理解时先当做方差）。

(2)P(n|n-1)是n时刻的方差矩阵的估计值，又由协方差自身性质，因此有如下公式：

4.2修正

卡尔曼滤波的核心公式，修正之前的估计值，得到当前时刻的最优估计值和最优最小均方误差矩阵。

4.2.1卡尔曼增益系数（误差增益）

注：K(n)为估计最小均方误差除以n时刻测量误差+估计最小均方误差，也就是估计误差占总误差的权重。

4.2.2修改后的估计值(第n时刻的最优估计值)：

注：x(n|n)是高斯融合后的最优估计误差均值，x(n|n-1)是估计误差均值，后面一项是由融合过程中推导出的增加量。我们先可以定性的分析一下。公式（5）K(n)较大时，即估计误差占比较大时，公式(6)中后一项数值相对也较大，也就是需要修改估计值的差值较大，也就说明了估计值比测量值误差大，因此数值要接近测量值。

4.2.3最小均方误差矩阵：

注：因为估计值被修改了，因此该估计值时刻的方差也应进行更新。

5.定性分析

假设有两个符合高斯分布的随机变量x,z，如下：

将两个概率密度函数相乘，得到：

将左式合并化简后，求出Up和方差：

如果令：

那么，（10）和（11）可表示为：

将公式（12）与（5）比较，（13）与（6）比较，（14）与（7）比较，可以发现他们的形式基本一致（令A=H=1），只不过5,6,7是多维矩阵推广形式。因此，我们也可以看出，卡尔曼增益稀疏是在化简过程中定义出来的变量。前面一直强调的，估计值就是误差的均值，最小均方误差就是误差的方差的概念，就是从这里得出的。

注：可以看出来高斯融合是有对称性的，也就是将x，z的位置对换公式也是成立的。现在的卡尔曼滤波器是以估计值作为基础的。如果，以观测值作为修改前的值，应该可以写出另一种滤波器的结构，感兴趣的同学可以继续研究。

另外：这么说看能不能解释清楚。你有两个秤称东西，假定东西重10kg（但是你不知道）。称重后，一个秤显示10.4kg，一个秤显示9.2kg。问你东西多重？于是假定相信秤1，60%，相信秤2，40%，最终结果9.92。理想状态下，最终的结果会更接近真实值。———————上述为一维问题，如果遇到多维就得套用kalman 滤波，而且还得分预测和更新两个模型计算。

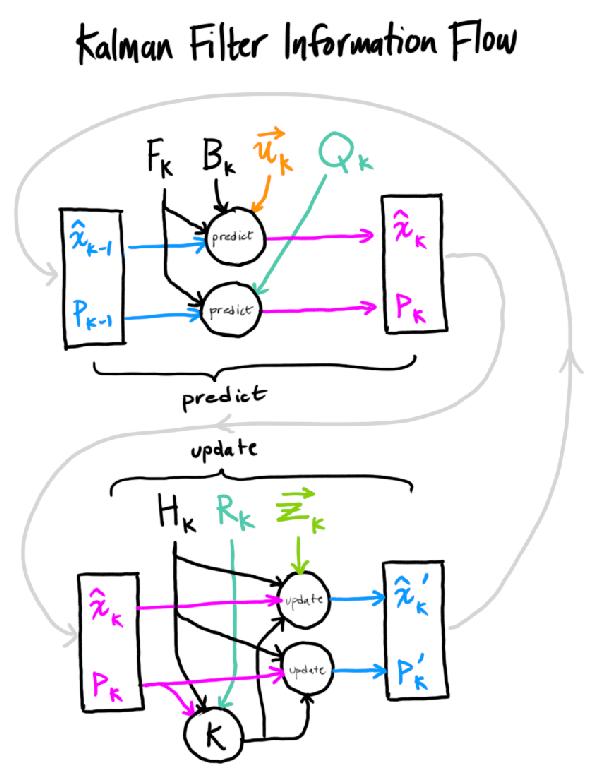
最简单的解释就是一图以蔽之：

卡尔曼滤波器是一种解方程的方法，是一种求后验均值的递推线性的求解方法。为什么要求后验均值？因为后验均值能让求解的未知数的误差(MSE)最小。有很多方法可以求后验均值，为什么卡尔曼这么流行？因为卡尔曼滤波最简单。