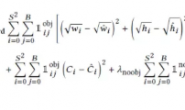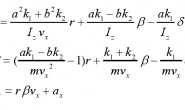最近做项目,谈到一个问题,有N个离散数据点,原来是采用线性回归的方式拟合出一条直线。但是客户提出一个问题:”你拟合的这个线不对啊,你看这些测试的数据点都不在线上,水平不行啊!”然后勒令乙方修改程序。。。作为程序员,只能按照客户的要求修改啊,做多项式拟合。客户还是不满意啊,你看,还有些点不在线上嘛!。。。
上述问题说明程序员不能脑子太死,这个问题本身就不用数学拟合,很简单,使用SPLINE算法就能解决了嘛。呵呵,而且还不能用B-spline,因为B-spline也是所有的点一起确定曲线的,spline曲线只是通过相邻的点确定曲线,所以spline绝对是通过所有的点的。
下面转贴一段spline算法程序。
/**
* @(#)TestLine.java
*
*
* @author
* @version 1.00 2012/7/12
*/
public class TestLine {
//标准曲线几个点坐标
double x[], y[];
double b[];//各点斜率
double c[];//凹凸面
double f[] = {0.14,0.16,0.18,0.22,0.26,0.28};//修正参数
//将坐标值初始赋值
public TestLine(double xx[], double yy[]) {
int n=xx.length;
x = new double[n];
y = new double[n];
for(int i=0; i<xx.length; i++){
x[i] = xx[i];
y[i] = yy[i];
}
}
//找到当前吸光度值所在的标准区线区间
public int getValueRange(double yy){
int tempN=-1;
for(int i=0; i<y.length-1; i++){
if(yy>y[i]&&yy<y[i+1]){
tempN=i;
}
}
if(tempN==-1){
for(int i=y.length-1; i>0; i–){
if(yy>y[i]&&yy<y[i-1]){
tempN=i;
}
}
//因为是从右边开始计数,所以需要减1
if(tempN>0)tempN–;
}
return tempN;
}
//采用直线方程计算未经修正的值
public double getFirstValue(double yy){
int tempN=getValueRange(yy);
double x1,x2,y1,y2;
x1=x[tempN];
x2=x[tempN+1];
y1=y[tempN];
y2=y[tempN+1];
//斜率
double k=(y2-y1)/(x2-x1);
double b=y1-k*x1;
double x3=(yy-b)/k;
return x3;
}
//计算曲线坐标点各点间的斜率
public void getXLValues(){
int n=x.length;
b = new double[n];
double x1,x2,y1,y2,k;
for(int i=0;i<n-1;i++){
x1=x[i];
x2=x[i+1];
y1=y[i];
y2=y[i+1];
//斜率
k=(y2-y1)/(x2-x1);
b[i]=k;
}
b[n-1]=0;
/**for(int i=0;i<n;i++){
System.out.println(“第”+i+”个=”+b[i]);
}**/
}
//修正算法
public double getFinalValue(double yy,double FirstValue){
int tempN=getValueRange(yy);
//超过一定数量默认值
double tempF=0.26;
if(tempN<5){
tempF=f[tempN];
}
System.out.println(“默认的修正参数”+tempF);
double x1,x2,x3;
x1=x[tempN];
x2=x[tempN+1];
//中间点值
x3=(x1+x2)/2;
double xz=(1-Math.abs(FirstValue-x3)/((x2-x1)/2))*tempF;
return FirstValue*(1-xz);
}
//找查计算值是不是等于标准曲线的点
public int getPointValue(double yy){
int tempN=-1;
for(int i=0;i<y.length;i++){
if(y[i]==yy)
tempN=i;
}
return tempN;
}
public static void main (String[] args){
double xx[] = {0,100,300,900,2700,8100};
//double yy[] = {2.296,1.902,1.407,0.591,0.180,0.060};
double yy[] = {0.06,0.18,0.591,1.407,1.902,2.296};
double value=0.16;
int tempN=0;
TestLine tl=new TestLine(xx,yy);
tempN=tl.getPointValue(value);
if(tempN>=0){
System.out.println(“要计算的吸光度直接与标准曲线对应的点等值,直接返回浓度”+xx[tempN]);
}else{
//如果不在标准曲线区间提示不能计算,需要重新做标准曲线
tempN=tl.getValueRange(value);
if(tempN==-1){
System.out.println(value+”超出了标准曲线的计算区间,请重新建立标准曲线!”);
}else{
double fv=tl.getFirstValue(value);
System.out.println(“直接计算结果”+fv);
System.out.println(“修正后结果”+tl.getFinalValue(value,fv));
}
}
}
}
测试数据如下:
1 37.67
2 8.54
3 5.53
4 1.59
6 2.57
8 0.89
10 3.61
12 1.33
14 1.37
16 2.89
18 0.94

图1是使用直线(straight)连接的,确实有点丑。
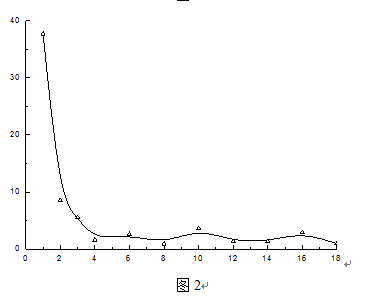
图2是用B-spline连接的。效果不错,但是有好多点不在曲线上,这个和我们客户的要求不符。
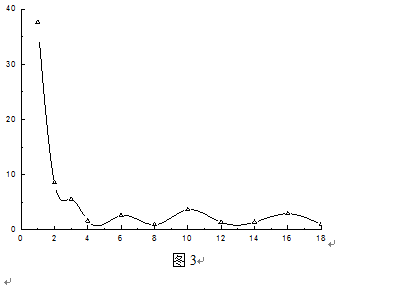
图3就是用spline连接的了,虽然难看了许多,但是满足要求了嘛。呵呵。
转载请注明:徐自远的乱七八糟小站 » 【原创】spline算法