IMU姿态融合（MPU9250从校正到滤波步骤）

联系方式：860122112@qq.com

一、动机

MPU9250包括三轴加速度计、三轴陀螺仪和三轴磁力计。因为加速度/磁力计具有高频噪声（需要低通滤波），将加速度/磁力计的信号看成是音频信号，它们的信号会有很多“毛刺“，也就是说它们的瞬时值不够精确，解算出来的姿态会震荡，但长期来看姿态方向是对的。而陀螺仪具有低频噪声（需要高通滤波），即每个时刻的得到的角速度是比较精确的，使用积分就能得到旋转角度（姿态），但是积分会累积误差，因此积分到后面姿态就不对了，也就是漂移现象。加速度/磁力计和陀螺仪在频域上的特性互补，可以融合这三种传感器的数据，提高精度和系统的动态特性。
下图表示的是把传感器翻转90°一段时间后又翻转回来时，加速度/磁力计、陀螺仪以及融合传感信号，所求得的姿态信息：

然而对于原始的MPU9250来说，在进行姿态融合前需要对传感器进行校正等“预处理”。

二、步骤

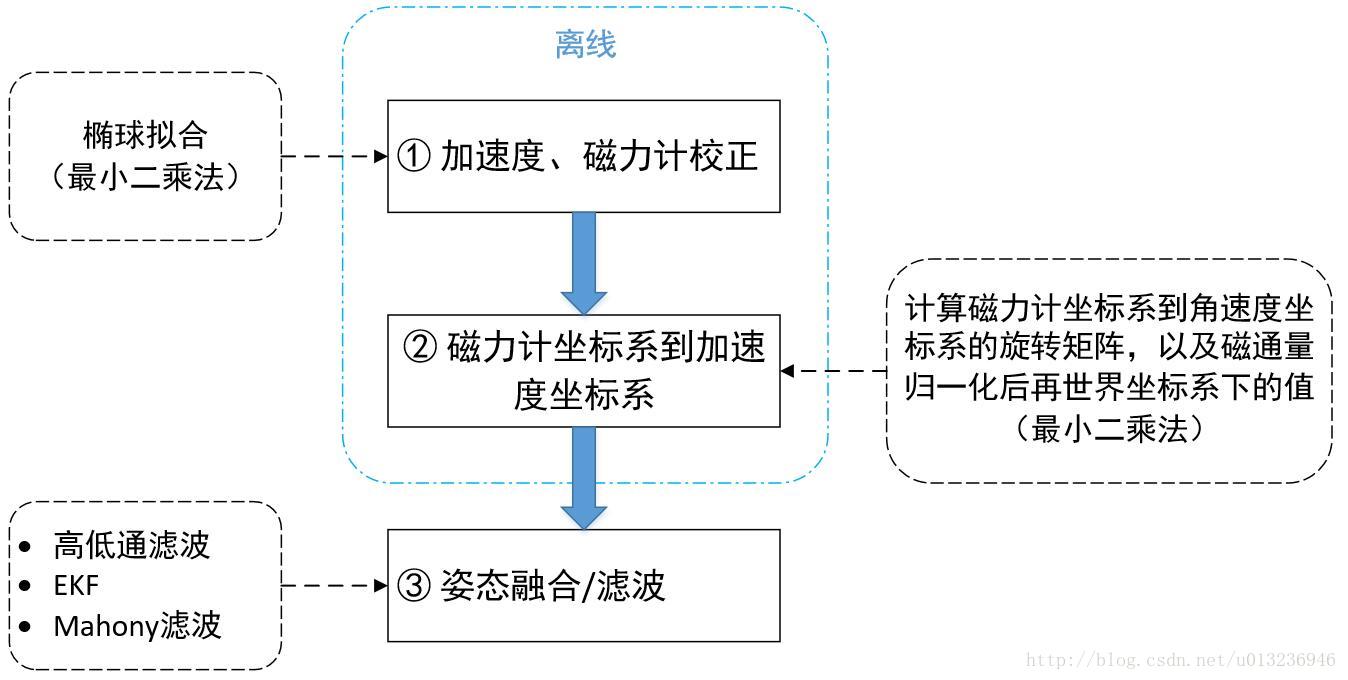
如上图所示，要对MPU9250进行姿态融合/滤波，大体需要三个步骤：1、校正，2、坐标转换，3、滤波。其中前两步需要离线执行。下面详解这三个步骤。

1. 传感器校正

按正常的情况来说，加速度传感器在静止状态（即只受重力作用），重力在各个姿态下，在三维空间中，向量顶点会落在一个球面上。但在IMＵ中，x,y,z轴的度量单位很大可能不相同，假设各轴之间相互直，各姿态重力点会落在一个椭球面上，椭球的中心也不一定在原点，这其实就是加速度的偏移量。

在磁力计上，由于测量磁场强度，在环境不变的情况下，传感器每个姿态感受磁场强度是相同的，所以不需要静止状态，磁力计测量的x,y,z轴值，在没有偏差且传感器内部x,y,z轴相互垂直的情况下，在三维空间中组成一个圆球面。但是磁力计存在Hard Iron Distortion和Soft Iron Distortion，使得x,y,z轴度量单位不相同，各轴也并非相互垂直，椭球球心也并非[0,0,0]坐标。

总的来说加速度/磁力计校正，需要求出椭球的球心（偏移量）、椭球轴长（各轴单位长度；其实磁力计不需要求，后面会解释。），即椭球拟合。

加速度计校正

在离线数据中寻找静止状态下的加速度传感器值，假设静止时的不同姿态共有 $n$ 个，则得到数据 $a c c D a t a \in R^{n \times 3}$ ；
$a c c D a t a \in R^{n \times 3}$ 作为样本数据，使用最小二乘法即可求出椭球方程的各个参数，接着根据我师兄博客的方法可以求出椭球的球心（偏移量）和轴长。

磁力计校正

提取离线数据的磁力计传感器的值（不需要静止状态），得到样本数据 $m a g D a t a \in R^{m \times 3}$ , 假设有m组数据；
$m a g D a t a \in R^{m \times 3}$ 作为样本数据，使用最小二乘法即可求出椭球方程的各个参数，进一步求出球心（偏移量）和轴长（轴长可忽略）。

陀螺仪校正

陀螺仪不存在椭球的问题，因此可以直接从离线数据中找到静止状态下的数据，对数据求均值即可得到偏移量。

2. 磁力计坐标系转换到加速度坐标系

磁力计的基坐标系和加速度的基坐标系（我们以加速度的基坐标系作为世界坐标系）并不一定是一样的，比如加速度的基坐标系x轴指向东，磁力计的指向北。因此，需要将磁力计坐标系转换到加速度计坐标系，才能通过加速度/磁力计解算出正确的姿态。

假设加速度计测量到的重力加速度向量是 $u_{g}$ ，磁力计测量到的磁通量是 $v_{m}$ ，首先要将 $v_{m}$ 从椭球上投射到正球上，投射方程为 $r_{m} = A v_{m}$ 。 $r_{m}$ 是投射后的向量， $A$ 为 $3 \times 3$ 的矩阵。

其次求出 $r_{m}$ 转换到加速度计坐标系的旋转矩阵 $R$ ，得到 $u_{m} = R r_{m}$ 。而无论任何情况磁通量 $u_{m}$ 和重力加速度 $u_{g}$ 的夹角固定，即 $u_{g} \cdot u_{m} = | u_{g} | \cdot | u_{m} | \cos θ$ , 因为我们只关心方向不关心大小，所以定值 $| u_{g} | \cdot | u_{m} | \cos θ$ 可归一化。综上，有

u g R A v m = 1

令 $B = R A$ 有

u g B v m = 1

椭球转换正球和旋转变换都已经包括在矩阵 $B$ 里了，再次使用最小二乘法求出 $B$ 的各个元素即可（对应前面，不必理会磁力计椭球的轴长）。

磁通量在世界坐标系下的x轴分量为0，重力加速度方向固定不变和z轴一致，通过向量点乘可以求出归一化后磁通量在世界坐标系下z轴的分量，再用模长公式求出y轴的分量。最后得到磁通量在世界坐标系下的向量 $w_{m}$ ，用于滤波时的校正。

3. 姿态融合

在使用各种滤波方法（如高低通滤波，EKF，Mahony）做姿态融合时，可以基于欧拉角、方向余弦和四元数等方法。欧拉角在求解姿态时存在奇点（万向节锁），不能用于全姿态解算；方向余弦可用于全姿态解算但计算量大，不能满足实时性要求；四元数，计算量小，无奇点，满足实时解算。

所以这里使用的是基于四元数姿态融合，滤波方法包括高低通滤波、EKF、Mahony滤波。下面简单介绍这三种算法的大致思想：

高低通滤波
两个方程说明问题

Q u a t e r n i o n (t) = (1 - α) Q u a t e r n i o n (t)^+ α \cdot a c c M a g Q u a t e r n i o n (t)

Q u a t e r n i o n (t)^= Q u a t e r n i o n (t - 1) g y r o S e n s o r Q (t)

$Q u a t e r n i o n$ 是姿态融合后的四元数， $g y r o S e n s o r Q$ 是陀螺仪测量到的角速度所代表的瞬时四元数， $\hat{Q u a t e r n i o n (t)}$ 是使用陀螺仪推算 $t$ 时刻的估计姿态， $a c c M a g Q u a t e r n i o n$ 是加速度/磁力计解算出的四元数。使用 $α$ 加权将陀螺仪的估算和加速度/磁力计的解算融合在一起，达到滤波效果。这里 $α = 0.1$ ，一般比较小，因为加速度/磁力计有高频噪声，需要低通滤波，否则会抖动。

EKF
广义卡尔曼滤波，主要有两步：估算、校正。（公式和推导不详述）。

估算：和高低通滤波一样，使用陀螺仪估算出 $t$ 时刻四元数；
校正：计算出估算姿态下的重力加速度和磁通量向量，再用加速度/磁力计测量到的重力加速度和磁通量向量按照EKF校正方程进行校正。

Mahony滤波
主要是使用了PI控制器思想（未深入，理解有偏差欢迎指出）。同样也分两步：估算、校正。

估算：和前面一样，使用陀螺仪估算出 $t$ 时刻四元数；
校正：计算出估算姿态下的重力加速度和磁通量向量，再用加速度/磁力计测量到的重力加速度和磁通量向量叉乘估算姿态的计算结果，得到的是估算姿态与测量姿态的误差 $e$ 。 $e$ 可以对陀螺仪测量到的角速度进行补偿，使用的是PI控制进行补偿。其中P用于控制加速度计和陀螺仪之间的交叉频率，I用于校正陀螺仪误差。使用补偿后的角速度重新估算出 $t$ 时刻四元数，此时已达到了滤波效果。

三、实验结果

加速度计椭球拟合

上图更像一个球，但球心明显偏离 $[0, 0, 0]$ 。

磁力计椭球拟合

同样球心明显偏离 $[0, 0, 0]$ 。

四元数姿态估计

下图中第一到第四行分别是四元数4个值在使用各种方法估计姿态时的变化情况，第五行是角速度的变化情况。

可以看到，除了Gyro估计的姿态，其他三种滤波算法估算的姿态基本一样。

Matlab实验视频：

前面两个图是加速度计和磁力计的椭球拟合；后一个图是各姿态融合算法对比，可以看到陀螺仪估算的姿态随时间累积误差变大，加速度/磁力计估算的姿态有明显的抖动（高频噪声），其他三种姿态融合算法效果差别不大。

计算时间 Mahony < 高低通 < EKF

手机端姿态融合
属于实验室张欣博士师兄的成果，非本人的工作。
<span data-mce-type="bookmark" style="display: inline-block; width: 0px; overflow: hidden; line-height: 0;" class="mce_SELRES_start"></span>

蓝牙传输的数据为100Hz

计算所用的时间 : Mahony < 高低通 < EKF

致谢：以上工作由张欣师兄指导完成，感谢师兄！

转载请注明：徐自远的乱七八糟小站 » IMU姿态融合（MPU9250从校正到滤波步骤）

徐自远的乱七八糟小站涉及电子，网络，编程，软件使用，机械结构等等方面。