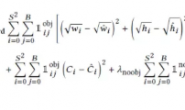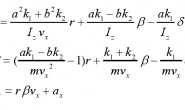【圆周率为什么碰巧是一个无理数,而且还是一个超越数呢?】
喜欢绞脑汁,故贸然闯入。不在乎露馅,求一吐为快,甘作嫁衣裳。我的奇葩解释如下。
数学是连续的无理数世界。数学追求的是“形的可分析性”与“数的可连续性”,二者互为因果。必须明白,可分析与可连续,只是“标准化建模”与“工具化机制”。数学思维的核心是“逼近”,这正是人类智慧的精髓。然而,真实世界的图景截然不同。
点“●”(x, y, z)。直线y=kx。抛物线y=ax²。圆x=ρcosθ, y=ρsinθ。螺线y=(1+1/x)^x…..这些形,点缀少量有理数,而见粗糙的断续;充塞大量的无理数,而见光滑的连续。

不只是圆,几何学的形位与形组,都对应一连串无理数。因此,圆对应π=3.141596…,螺线对应e=2.71828…,正方对角线√2=1.412…,邻域对应差分Δx或微分dx……等都是无理数,都是极大概率事件,而绝非巧合。
物理是离散的有理数世界。物理玩的是量子与概率,测量精度只需到有理数与虚数。能量是一份一份,分能级的。电荷是一个一个,最精密到分数(夸克电荷)。角动量是整数或半整数(0,1,2,3,4,1/2,3/2)不存在或不必要无理数或超越数,包括无穷小(1/∞)与无穷大(∞)。