导读：在开始使用TensorFlow之前，必须了解它背后的理念。该库很大程度上基于计算图的概念，除非了解它们是如何工作的，否则无法理解如何使用该库。本文将简要介绍计算图，并展示如何使用TensorFlow实现简单计算。

作者：翁贝托·米凯卢奇（Umberto Michelucci）

来源：大数据DT（ID：bigdatadt）

01 计算图

要了解TensorFlow的工作原理，必须了解计算图是什么。计算图是一幅图，其中每个节点对应于一个操作或一个变量。变量可以将其值输入操作，操作可以将其结果输入其他操作。

通常，节点被绘制为圆圈，其内部包含变量名或操作，当一个节点的值是另一个节点的输入时，箭头从一个节点指向另一个节点。可以存在的最简单的图是只有单个节点的图，节点中只有一个变量。（请记住，节点可以是变量或操作。）图1-16中的图只是计算变量x的值。

▲图1-16 我们可以构建的最简单的图，它表示一个简单的变量

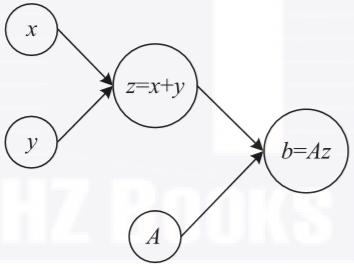
现在让我们考虑稍微复杂的图，例如两个变量x和y之和（z=x+y），如图1-17所示。

▲图1-17 两个变量之和的基本计算图

图1-17左侧的节点（圈里有x和y的节点）是变量，而较大的节点表示两个变量之和。箭头表示两个变量x和y是第三个节点的输入。应该以拓扑顺序读取（和计算）图，这意味着你应该按照箭头指示的顺序来计算不同的节点。箭头还会告诉你节点之间的依赖关系。要计算z，首先必须计算x和y。也可以说执行求和的节点依赖于输入节点。

要理解的一个重要方面是，这样的图仅定义了对两个输入值（在这里为x和y）执行什么操作（在这里为求和）以获得结果（在这里为z）。它基本上定义了“如何”。你必须为x和y这两个输入都赋值，才能执行求和以获得z。只有在计算了所有的节点后，图才会显示结果。

注释：在本书中，图的“构造”阶段是指在定义每个节点正在做什么时，“计算”阶段是指当我们实际计算相关操作时。

这是需要了解的一个非常重要的方面。请注意，输入变量不一定是实数，它们可以是矩阵、向量等。（本书中主要使用矩阵。）在图1-18中可以找到稍微复杂的示例，即给定三个输入量x、y和A，使用图计算A(x+y)的值。

▲图1-18 给定三个输入量x、y和A，计算A(x+y)的值的计算图

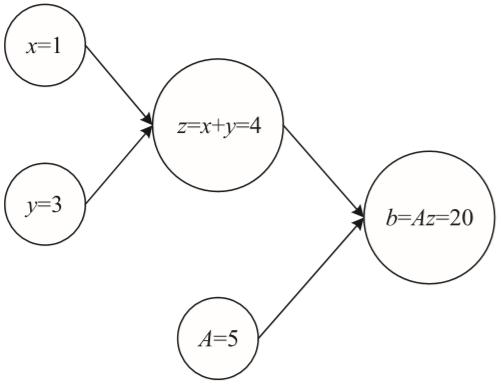
可以通过为输入节点（在本例中为x、y和A）赋值来计算此图，并通过图计算节点。例如，如果采用图1-18中的图并赋值x=1、y=3和A=5，将得到结果b=20（如图1-19所示）。

▲图1-19 要计算图1-18中的图，必须为输入节点x、y和A赋值，然后通过图计算节点

神经网络基本上是一个非常复杂的计算图，其中每个神经元由图中的几个节点组成，这些节点将它们的输出馈送到一定数量的其他神经元，直到到达某个输出。

TensorFlow可以帮助你非常轻松地构建非常复杂的计算图。通过构造，可以将评估计算与构造进行分离。（请记住，要计算结果，必须赋值并计算所有节点。）

注释：请记住，TensorFlow首先构建一个计算图（在所谓的构造阶段），但不会自动计算它。该库将两个步骤分开，以便使用不同的输入多次计算图形。

02 张量

TensorFlow处理的基本数据单元是张量（Tensor），它包含在TensorFlow这个单词中。张量仅仅是一个形为n维数组的基本类型（例如，浮点数）的集合。以下是张量的一些示例（包括相关的Python定义）：

• 1→一个纯量
• [1,2,3]→一个向量
• [[1,2,3], [4,5,6]]→一个矩阵或二维数组

张量具有静态类型和动态维度。在计算它时，不能更改其类型，但可以在计算之前动态更改维度。（基本上，声明张量时可以不指定维度，TensorFlow将根据输入值推断维度。）通常，用张量的阶（rank）来表示张量的维度数（纯量的阶可以认为是0）。表1-1可以帮助理解张量的不同阶。

▲表1-1 阶为0、1、2和3的张量示例

假设你使用语句import TensorFlow as tf导入TensorFlow，则基本对象（张量）是类tf.tensor。tf.tensor有两个属性：

• 数据类型 （例如，float32）
• 形状（例如，[2,3]表示这是一个2行3列的张量）

一个重要的方面是张量的每个元素总是具有相同的数据类型，而形状不需要在声明时定义。主要张量类型（还有更多）有：

• tf.Variable
• tf.constant
• tf.placeholder

tf.constant和tf.placeholder值在单个会话运行期间（稍后会详细介绍）是不可变的。一旦它们有了值，就不会改变。例如，tf.placeholder可以包含要用于训练神经网络的数据集，一旦赋值，它就不会在计算阶段发生变化。

tf.Variable可以包含神经网络的权重，它们会在训练期间改变，以便为特定问题找到最佳值。最后，tf.constant永远不会改变。我将在下一节展示如何使用这三种不同类型的张量，以及在开发模型时应该考虑哪些方面。

03 创建和运行计算图

下面开始使用TensorFlow来创建计算图。

注释：请记住，我们始终将构建阶段（定义图应该做什么）与它的计算阶段（执行计算）分开。TensorFlow遵循相同的理念：首先构建一个图形，然后进行计算。

考虑非常简单的事情：对两个张量求和，即

x1+x2

可以使用图1-20的计算图来执行计算。

▲图1-20 求两个张量之和的计算图

04 包含tf.constant的计算图

如前所述，首先必须使用TensorFlow创建这个计算图。（记住，我们从构建阶段开始。）让我们开始使用tf.constant张量类型。我们需要三个节点：两个用于输入变量，一个用于求和。可以通过以下代码实现：

以上代码创建图1-20中的计算图，同时，它告诉TensorFlow：x1的值是1（声明中括号内的值），而x2的值为2。现在，要执行代码，我们必须创建被TensorFlow称为会话的过程（实际的计算过程就在其中进行），然后可以请求会话类通过以下代码运行我们的图：

这将简单地提供z的计算结果，正如所料，结果是3。这部分代码相当简单且不需要太多，但不是很灵活。例如，x1和x2是固定的，并且在计算期间不能改变。

注释：在TensorFlow中，首先必须创建计算图，然后创建会话，最后运行图。必须始终遵循这三个步骤来计算你的图。

请记住，也可以要求TensorFlow仅计算中间步骤。例如，你可能想要计算x1，比如sess.run(x1)（虽然在这个例子中没什么意义，但是在很多情况下它很有用，例如，如果想要在评估图的同时评估模型的准确性和损失函数）。

你会得到结果1，正如预期的那样。最后，请记住使用sess.close()关闭会话以释放所用资源。

05 包含tf.Variable的计算图

可以使用相同的计算图（图1-20中的图）来创建变量，但这样做有点麻烦，不如让我们重新创建计算图。

我们像之前一样用值1和2进行变量初始化。问题在于，当使用以下代码运行此图时，将收到一条报错消息。

这是一条非常长的消息，但消息的结尾包含以下内容：

发生这种情况是因为TensorFlow不会自动初始化变量。为此，你可以使用此办法：

现在没有错误了。sess.run(x1.initializer)这行代码将使用值1初始化变量x1，而sess.run(x2.initializer)将使用值2初始化变量x2，但这相当麻烦。（你也不希望为每个需要初始化的变量写一行代码。）更好的方法是在计算图中添加一个节点，以便使用如下代码初始化在图中定义的所有变量：

然后再次创建并运行会话，并在计算z之前运行此节点（init）。

以上代码很有效，如你所料，输出了正确结果3。

注释：使用变量时，请记住一定要添加全局初始化器（tf.global_variables_initializer()），并在一开始就在会话中运行该节点，然后再进行任何其他计算。我们将在本书的许多例子中看到它是如何工作的。

06 包含tf. placeholder的计算图

我们将x1和x2声明为占位符：

请注意，我没有在声明中提供任何值。我们将不得不在计算时为x1和x2赋值。这是占位符与其他两种张量类型的主要区别。然后，再次用以下代码执行求和：

请注意，如果尝试查看z中的内容，例如print(z)，你将得到：

为何得到这个奇怪的结果？首先，我们没有给TensorFlow提供x1和x2的值，其次，TensorFlow还没有运行任何计算。请记住，图的构造和计算是相互独立的步骤。现在我们像之前一样在TensorFlow中创建一个会话。

现在可以运行实际的计算了，但要做到这一点，必须先为x1和x2两个输入赋值。这可以通过使用一个包含所有占位符的名称作为键的Python字典来实现，并为这些键赋值。在此示例中，我们将值1赋给x1，将值2赋给x2。

可以通过使用以下命令将上面的代码提供给TensorFlow会话：

终于得到了期望的结果：3。注意，TensorFlow相当聪明，可以处理更复杂的输入。让我们重新定义占位符，以便使用包含两个元素的数组。（在这里，我们给出完整的代码，以便更容易跟进该示例。）

这次，将得到一个包含两个元素的数组作为输出。

请记住，x1=[1,5]和x2=[1,1]意味着z=x1+x2=[1,5]+[1,1]=[2,6]，因为求和（sum）是对数组中逐元素求和得到的。

总结一下，下面是一些关于何时使用哪种张量类型的指南：

• 对于在计算阶段不发生更改的实体，请使用tf.placeholder。通常，它们是你希望在计算期间保持固定不变的输入值或参数，但可能随每次运行而变化。（你将在本书后面看到几个示例。）示例包括输入数据集、学习率等。
• 对于在计算过程中会发生变化的实体，请使用tf.Variable，例如，神经网络的权重，本书后面将对此进行介绍。
• tf.constant用于永不更改的实体，例如，那些在模型中不再更改的固定值。

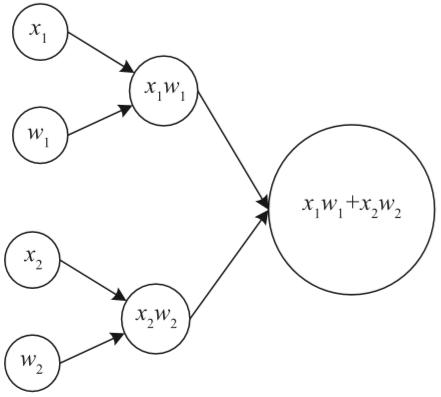
图1-21描绘了一个稍微复杂的例子：计算x1w1+x2w2的计算图。

▲图1-21 计算x1w1+x2w2的计算图

在这个例子中，我将x1、x2、w1和w2定义为包含纯量的占位符（它们将是输入）（记住：在定义占位符时，必须始终将维度作为第二个输入参数传入，在本例中是1）。

运行该计算也就意味着（如前所述）：定义包含输入值的字典，之后创建会话，然后运行它。

不出所料，你将获得以下结果：

这很简单，即1×2+3×4=2+12=14（记住，在前一步骤中已经在feed_dict中输入了值1、2、3和4）。与往常一样，请记得在完成后用sess.close()关闭会话。

注释：在TensorFlow中，可能会发生同一段代码运行多次，并且最终会得到一个包含同一节点的多个副本的计算图。避免此类问题的一种非常常见的方法是在运行构造该图的代码之前先运行代码tf.reset_default_graph()。请注意，如果你将构造代码与计算代码恰当地分开了，则应该能够避免此类问题。我们将在本书后面的许多例子中看到它是如何工作的。

关于作者：翁贝托·米凯卢奇（Umberto Michelucci），目前在瑞士领先的医疗保险公司从事创新和人工智能（AI）工作。他领导与人工智能、新技术、机器学习以及大学的研究合作相关的多项战略计划。此前，他曾担任多个大型医疗保健项目的数据科学家和首席建模师，并在编程和算法设计方面拥有丰富的实践经验。他管理过商务智能和数据仓库项目，使数据驱动的解决方案能够在复杂的生产环境中实施。

本文摘编自《深度学习：基于案例理解深度神经网络》，经出版方授权发布。

延伸阅读《深度学习：基于案例理解深度神经网络》

推荐语：本书探讨了深度学习中的高级主题，例如优化算法、超参数调整、Dropout和误差分析，以及解决在训练深度神经网络时遇到的典型问题的策略。你首先要研究激活函数，主要是单个神经元（relu、sigmoid和swish），了解如何使用TensorFlow进行线性和逻辑回归，并选择正确的代价函数。

TensorFlow是什么？怎么用？终于有人讲明白了http://t.zijieimg.com/QGuduA/

转载请注明：徐自远的乱七八糟小站 » TensorFlow是什么？怎么用？终于有人讲明白了