在上一节，我们主要讲解了替代损失（Surrogate loss）由来和性质，明白了机器学习中损失函数定义的本质，我们先对回归任务总结一下常用的损失函数：

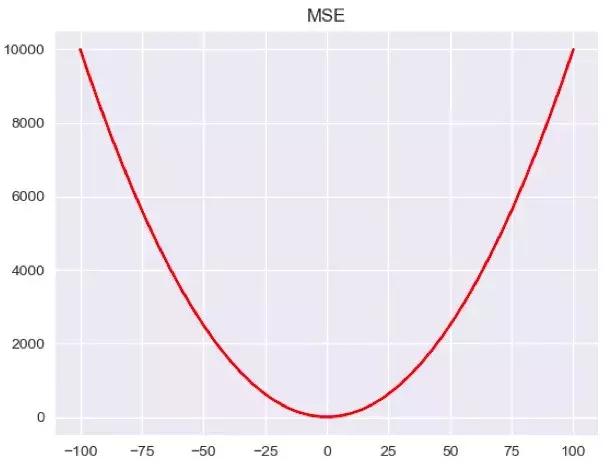
• 均方误差（MSE）：

import numpy as np

def MSE(true, pred):

return (true – pred)**2

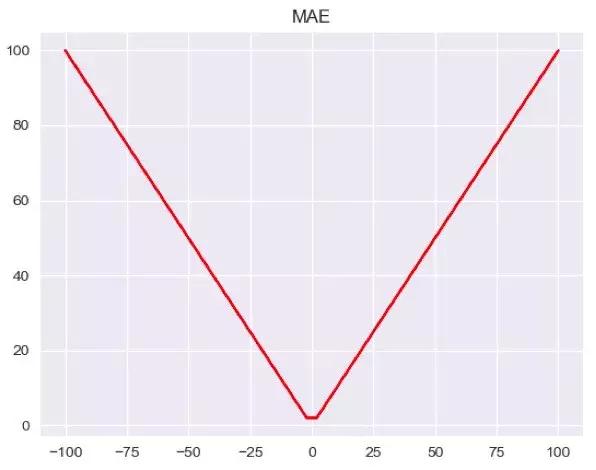
• 绝对误差（MAE）：

import numpy as np

def MAE(true, pred):

return np.abs(true – pred)

• HuberLoss:

import numpy as np

def Huber(true, pred,e):

a=np.abs(true-pred)

return np.array([0.5*i**2 if i<e else e*i-0.5*e**2 for i in a ])

其中，MSE和MAE都是比较熟悉且简单的损失函数，MSE对预测值和真实值的差取了平方，当出现异常值的时候，就会放大相应的Loss，而MAE只是取到预测值和真实值的绝对值。换而言之，异常值会在MSE中占到更大的比例，这样并不合理。我们可以画出简单的图像：

……

a=np.linspace(-100,100)

sns.set(style=’darkgrid’)

plt.plot(a,MSE(0,a),’r-‘)

plt.title(‘MSE’)

plt.show()

……

……

plt.plot(a,MAE(0,a),’r-‘)

……

从图中可以看出，同样是数值为100的点，MSE的Loss会更大,当我们把这些全部加起来得到总体的Loss，数值与真实值偏离越大的比重也会越大。

……

a=np.linspace(0,100)

sns.set(style=’darkgrid’)

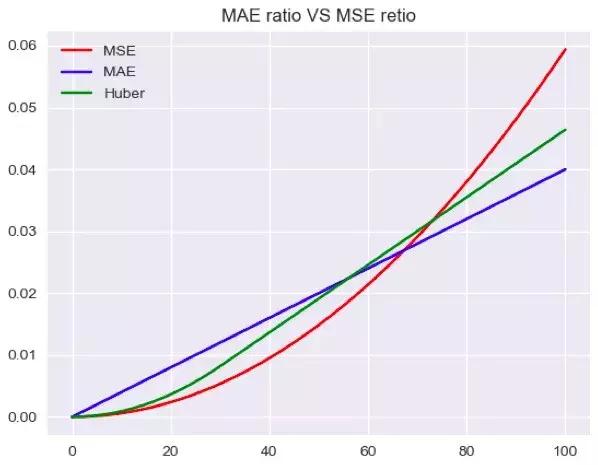
plt.plot(a,MSE(0,a)/np.sum(MSE(0,a)),’r-‘)

plt.plot(a,MAE(0,a)/np.sum(MAE(0,a)),’b-‘)

plt.title(‘MAE ratio VS MSEretio’)

plt.show()

……

可以直观的看到，随着偏离真实值的程度增大，异常点所产生的loss的比重也会增大。

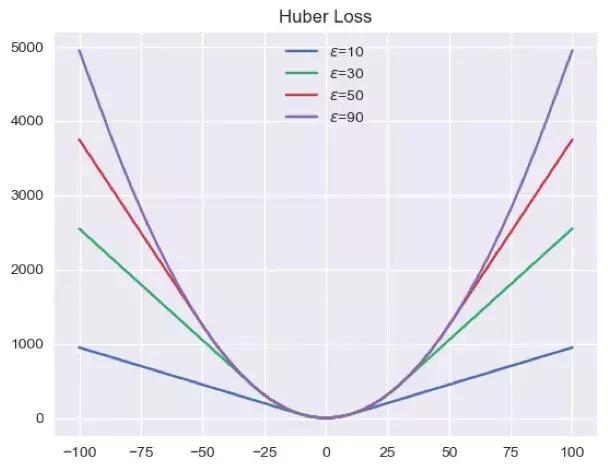
从这样看来，MAE似乎是更好的损失函数，使得最后的结果不会偏向于异常值，但是MAE的导数是个常数，使得每次的梯度更新时，都下降同样的长度，这不能保证我们得到满意的结果。Huber Loss虽然看起来很复杂，但实际上只是MSE和MAE的折中，因为它定义了一个参数，这个参数的主要作用是判断一个数据点是否是异常值，当我们的预测值距离真实值较远时，我们选用MSE，反之，就利用MAE，我们尝试调节参数看其在target所张成空间中的形状：

……

for i in [10,30,50,90]:

plt.plot(a,Huber(0,a,i))

plt.title(‘Huber Loss’)

plt.show()

如图，我们可以看到随着的增加，huber loss越来越像MSE，这是因为参数的变大，意味着异常点越来越少。

同时我们也可以预料到，huber loss中偏离越大的点占据的比重应该介于两者之间：

plt.plot(a,Huber(0,a,30)/np.sum(Huber(0,a,30)),’g-‘,label=’Huber’)

既然huber loss可以适应异常点，那么我们构建一个含有异常点的数据，用简单的线性回归作为模型，采用不同的loss function，观察它找出的线性回归模型的差异在哪里。首先，我们构建包含异常点的数据：

import numpy as np

from sklearn.datasets import make_regression

rng = np.random.RandomState(0)

X, y =make_regression(n_samples=50, n_features=1, random_state=0, noise=4.0,

bias=100.0)

sns.set(style=’darkgrid’)

X_outliers = rng.normal(0, 0.5, size=(4, 1))

y_outliers = rng.normal(0, 2.0, size=4)

X_outliers[:2, :] += X.max() + X.mean() /4.

X_outliers[2:, :] += X.min() – X.mean() /4.

y_outliers[:2] += y.min() – y.mean() /4.

y_outliers[2:] += y.max() + y.mean() /4.

X = np.vstack((X,X_outliers))

y = np.concatenate((y,y_outliers))

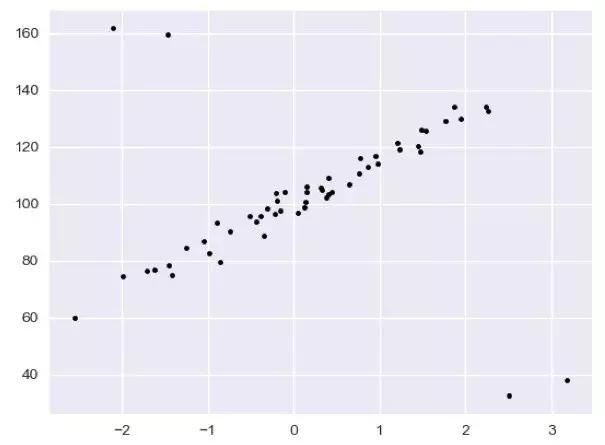
plt.plot(X, y, ‘k.’)

plt.show()

如图，我们可以很清晰的看到中间的样本点是近乎完美的线性，但在左上方和右下放却出现了一些异常点。

我们分别构建普通最小二乘的loss（MSE）、ridge regression的loss（MSE+）,以及huber loss来观察在样本空间会形成怎样的结果：

from sklearn.linear_model import HuberRegressor,Ridge

from sklearn.linear_model import LinearRegression

x = np.linspace(X.min(), X.max(), 100)

huber =HuberRegressor(fit_intercept=True, alpha=0.0, max_iter=100,epsilon=1.5)

huber.fit(X, y)

coef_ = huber.coef_ * x + huber.intercept_

plt.plot(x,coef_,’r-‘,label=”huber loss, %s”%1.5)

ridge = Ridge(fit_intercept=True, alpha=3, random_state=0, normalize=True)

ridge.fit(X, y)

coef_ridge = ridge.coef_

coef_ = ridge.coef_ * x + ridge.intercept_

plt.plot(x,coef_, ‘g-‘, label=”ridge regression”)

ols =LinearRegression(fit_intercept=True, normalize=True)

ols.fit(X, y)

coef_ols = ols.coef_

coef_ =ols.coef_ * x + ols.intercept_

plt.plot(x,coef_, ‘b-‘, label=”linear regression”)

plt.title(“Comparison ofHuberRegressor vs Ridge”)

plt.xlabel(“X”)

plt.ylabel(“y”)

plt.legend()

plt.show()

如图，OLS和Ridge regression 都不同程度上受到了异常点的影响，而huber loss却没有受任何影响。

如果我们只是看这幅图，也不会觉得huber loss有多么厉害，因为OLS和Ridge regression的偏差也不是很大。这里面的很大一部分原因是异常点的偏离还不是很大，或者正常的点占的比重还是比较大，我们接下来减小正常点的个数：

X, y = make_regression(n_samples=15, n_features=1, random_state=0,noise=4.0,

bias=100.0)

如图，正常点所占的比重越小，普通的Loss就无法适应，它所决定出的回归方程几乎没有什么预测能力。

面对分类问题，我们是不是也可以选择不同的loss function使得效果更好呢？分类任务中，我们常用：

• 负对数损失：

def cross_entropy(predictions, targets, epsilon=1e-10):

predictions = np.clip(predictions,epsilon, 1.- epsilon)

N = predictions.shape[0]

ce_loss =-np.sum(np.sum(targets * np.log(predictions +1e-5)))/N

return ce_loss

• hingeloss：

def hinge(y,f):

return max(1-y*f)

我们分别选用这两种Loss，其实也对应着linear SVM和logistic regression，然后在IRIS数据利用随机梯度下降的算法观察决策边界的变化：

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets

from sklearn.linear_model import SGDClassifier

iris = datasets.load_iris()

X = iris.data[:, :2]

y = iris.target

colors =”bry”

idx = np.arange(X.shape[0])

np.random.seed(13)

np.random.shuffle(idx)

X = X[idx]

y = y[idx]

mean = X.mean(axis=0)

std = X.std(axis=0)

X = (X – mean) / std

h =.02

clf = SGDClassifier(loss=’log’,alpha=0.01, max_iter=100).fit(X, y)

x_min, x_max = X[:, 0].min() -1, X[:, 0].max() +1

y_min, y_max = X[:, 1].min() -1, X[:, 1].max() +1

xx, yy =np.meshgrid(np.arange(x_min, x_max, h),

np.arange(y_min, y_max,h))

Z =clf.predict(np.c_[xx.ravel(), yy.ravel()])

Z = Z.reshape(xx.shape)

cs = plt.contourf(xx, yy,Z, cmap=plt.cm.RdBu,alpha=0.6)

plt.axis(‘tight’)

for i, color in zip(clf.classes_, colors):

idx = np.where(y == i)

plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],

cmap=plt.cm.RdBu, edgecolor=’black’, s=20,edgecolors=’k’)

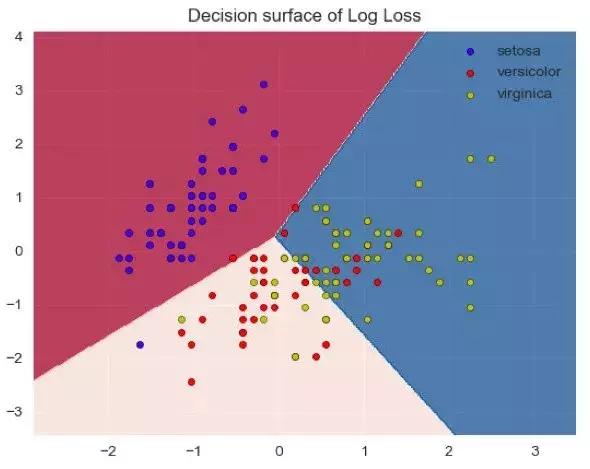
plt.title(“Decision surfaceof Log Loss”)

plt.axis(‘tight’)

plt.show()

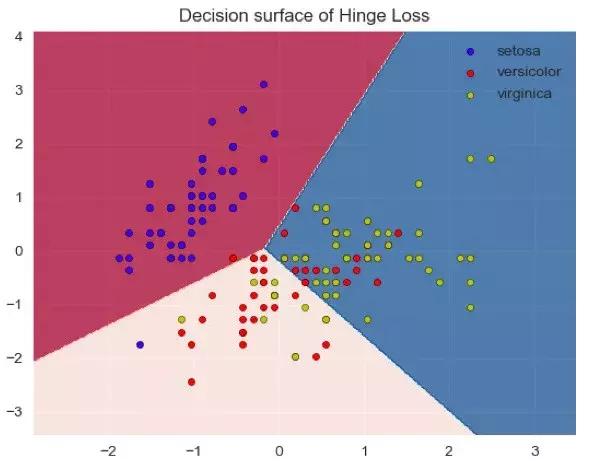
同样，我们可以画出hinge loss:

clf = SGDClassifier(loss=’hinge’,alpha=0.01, max_iter=100).fit(X, y)

从图中我们无法说明哪一个loss是更好的，一方面对于这样简单的数据，可能loss并不起主要作用，另一方面，我们需要观察测试集的泛化误差来确定，这里面只是两个特征所构成的空间。

注意到我们在这里添加了L2正则化,除此之外，我们还可以自由的添加L1正则化和弹性网（结合两类正则化），作为我们的结构风险项。总之，在替代损失结构之中，我们只需要让其具备连续性和一致性(凸函数不是必要的)，就是合理的，所以我们完全可以根据自己的数据和任务去设计更灵活的loss function。

读芯君开扒

课堂TIPS

• 除了MSE，MAE，huber loss，在回归任务中，我们还会使用log-cosh loss，它可以保证二阶导数的存在，有些优化算法会用到二阶导数，在xgboost中我们同样需要利用二阶导数；同时，我们还会用到分位数损失，希望能给不确定的度量。

• 除了log和hinge，在分类任务中，我们还有对比损失（contrastive loss）、softmax cross-entropy loss、中心损失（center loss）等损失函数，它们一般用在神经网络中。

• lossfunction多样性的背后实际上是靠着一类叫做随机梯度下降（SGD）的优化算法作为支撑，随机梯度下降的优越性绝不是为了减小时间效率，而是机器学习伟大的创新之一，我们将在下一节介绍以SGD为代表的优化算法。

• 均方误差（MSE）：是回归问题中最常被使用的损失函数。