受过训练以对图像进行分类的神经网络具有非凡的意义和惊人的生成图像的能力。诸如 DeepDream,风格迁移和特征可视化等技术利用这种能力作为探索神经网络内部工作的强大工具,并为基于神经艺术的小型艺术运动提供动力。
所有这些技术的工作方式大致相同。计算机视觉中使用的神经网络具有它们所看到的图像的丰富内部表示。我们可以使用此表示来描述我们希望图像具有的属性(例如样式),然后优化输入图像以具有这些属性。这种优化是可能的,因为网络在输入方面是可区分的:我们可以稍微调整图像以更好地适应所需的属性,然后在梯度下降中迭代地应用这种调整。
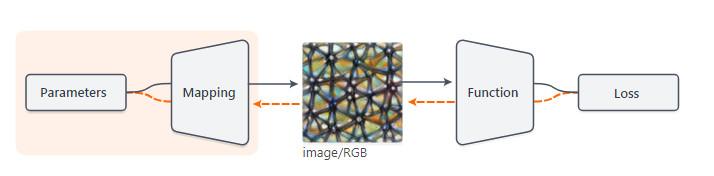
通常,我们将输入图像参数化为每个像素的 RGB 值,但这不是唯一的方法。只要从参数到图像的映射是可微分的,我们仍然可以使用梯度下降来优化可选的参数化方式。
1:只要图像参数化是可微分的,那我们就可以对其进行反向传播。
可微分的图像参数化不禁让我们想问:我们可以反向传播什么样的图像生成过程?答案很多,甚至有一些可以产生各种有趣的效果,包括 3D 神经艺术,具有透明度的图像以及对齐插值。之前使用特定异常图像参数化的工作已经显示出令人兴奋的结果,我们认为缩小并整体观察这个区域表明,其中还存在着更多的潜力尚待挖掘。
为什么参数化很重要?
尽管实际优化后目标函数保持不变,但改变优化问题的参数化可能会显著改变结果,这似乎令人惊讶。以下是参数化的选择可能产生重大影响的四个原因:
- 改进后的优化:转换输入以使优化问题更容易,即被称为「预处理」的技术,是优化的主要内容。预处理通常表现为梯度的变换(通常将其乘以正定的「预处理器」矩阵)。但是,这相当于优化输入的备用参数化。我们发现参数化的简单变化使得神经艺术的图像优化和图像优化变得更加容易。
- 吸引盆:当我们优化对神经网络的输入时,通常存在许多不同的解决方案,分别对应于不同的局部最小值。训练以复杂优化场景图(landscapes)为特征的深度神经网络,其对于给定目标可具有许多同样良好的局部最小值。(请注意,找到全局最小值并不总是可取的,因为它可能会导致模型过拟合。)因此,优化神经网络的输入也会产生许多局部最小值,这并不奇怪。我们的优化过程落入任何特定局部最小值的概率由其吸引力盆地(即,在最小值的影响下的优化场景图的区域)控制。已知改变优化问题的参数化会改变不同吸引盆的大小,从而影响可能的结果。
- 附加约束:一些参数化仅涵盖可能输入的子集,而不是整个空间。在这样的参数化中工作的优化器仍将找到最小化或最大化目标函数的解决方案,但它们将受到参数化的约束。通过选择正确的约束集,可以施加各种约束,范围从简单约束(例如,图像的边界必须是黑色)到丰富的细微约束。
- 隐式优化其他对象:参数化可以在内部使用与其输出的对象以及我们所要优化的对象不同的对象。例如,虽然视觉网络的自然输入是 RGB 图像,但我们可以将该图像参数化为 3D 对象的渲染,并且通过在渲染过程中反向传播来优化该图像。因为 3D 对象具有比图像更多的自由度,所以我们通常使用随机参数化来生成从不同视角渲染的图像。
在本文的其余部分,我们给出了具体的例子,这些方法都很有用,都能产生令人惊讶和有趣的视觉效果。
第一部分:对齐特征可视化插值
特征可视化最常用于可视化单个神经元,但它也可用于可视化神经元的组合,以研究它们如何相互作用。目的不是优化图像以激活单个神经元,而是优化它来激活多个神经元。
当我们想要真正理解两个神经元之间的相互作用时,我们可以更进一步,创建多个可视化,逐渐将目标从优化一个神经元转移到对其他神经元激活的加权。这在某些方面类似于像 GAN 这样的生成模型的潜在空间中的插值。
尽管如此,还是存在一个小挑战:特征可视化是随机的。即使你针对完全相同的目标进行优化,每次都会以不同的方式呈现出可视化结果。通常,这不是问题,但它确实减损了插值可视化。如果我们不加思索地进行处理,所得到的可视化将是不对齐的:诸如眼睛的视觉位置出现在每个图像中的不同位置。这种缺乏对齐可能会因为目标略有不同而难以看出差异,因为它们被布局中更大的差异所淹没。
如果我们将插值帧看作动画,我们可以看到独立优化的问题:
2
我们如何实现这种对齐插值,其中视觉位置不在帧之间移动?可以尝试许多可能的方法。例如,可以明确地惩罚相邻帧之间的差异。我们的最终结果和我们的 colab notbook 将此技术与共享参数化结合使用。其中一个是使用共享参数化:每个帧被参数化为其自己的唯一参数化和单个共享参数化的组合。
3
通过在框架之间部分共享参数化,我们尽可能使生成的可视化自然对齐。直观上感觉,共享参数化为视觉标志的位移提供了公共参考,而独特的参数化基于其插值权重给予每个帧其自身的视觉吸引力。此参数化不会更改目标,但它会扩大可视化对齐的吸引力盆地。
这是一个初始的例子,说明了可区分参数化通常是如何成为可视化神经网络的有用的附加工具的。
第二部分:非 VVG 架构下的风格迁移
神经风格迁移一直以来都有一个未解之谜:尽管它已经取得显著的成功,但几乎所有的风格迁移都是依赖于 VGG 架构完成的。这并不是因为没有人对基于其他体系结构的风格转移感兴趣,而是因为不断的尝试过后发现效果都很差。在 Medium、 Reddit 和 Twitter 上都可以找到用不同架构进行实验的例子。
如今已经提出了几个假设来解释为什么在 VGG 架构上工作会比在其他模型上效果好得多。一种解释是由于 VGG 架构有比较大的规模去获取其他模型丢失的信息,这些信息即使说对分类没什么帮助,但是它确实能够使得该模型更好的完成风格迁移。另一种解释是其他模型相比于 VGG 模型更具有攻击性,这也导致其失去空间信息。我们认为可能还有另外一个因素:大多数现代视觉模型在梯度上都有棋盘状伪影,这可能使程式化图像在进行优化时变得更加困难。
在之前的工作中,我们发现解相关的参数化可以明显提高优化效果,同时这种方法也可以改善风格迁移。在这里请允许我们使用一个没有产生视觉吸引力的风格迁移模型:
4:移动最终优化图像下的滑块,将像素空间中的优化效果与非相关空间中进行比较。这两张图像是在同一个目标下创建的,它们的区别仅在于参数化的不同。
让我们更全面地去思考这个改变。风格迁移涉及三种图像:内容图像、风格图像以及我们优化后的图像。这三种图像都要放入卷积神经网络中,风格迁移物体与其他的不同之处是在于激活卷积运算的的方式不同。我们唯一的改变是如何将优化后的图像参数化。相对于用像素级别的参数化(这种方法易受邻近像素点的影响),我们采用缩放的傅里叶变换进行参数化。
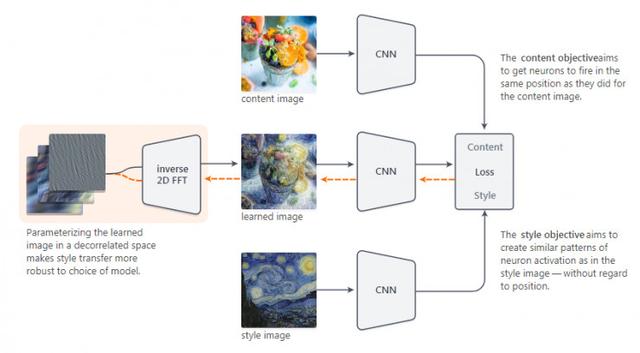
5: 在去相关领域中的图像使得风格迁移对模型的选择更加稳定。内容目标旨在让神经元与内容图像在同样的位置上做出标记。风格目标致力于创建类似于风格图像中的神经元激活模式(不考虑位置关系)。这与二维傅里叶变换相反。
我们精确的实行方法可在附录中查看。注意该方法也使用了迁移稳定性,这种稳定性并不适用于所有的风格迁移。
第三部分:复合模式生成网络
至今为止,我们已经研究了使用像素或傅里叶方法进行参数化,这些参数化程度与我们通常对图像的认知比较接近。在该节中我们探讨了通过使用不同的参数化将额外约束添加到优化过程的可能性。更确切的说,我们将图像当成神经网络一样进行参数化,特别是复合模式生成网络。
复合模式生成网络是将(x,y)位置映射到图像颜色中的神经网络。
将复合模式生成网络应用到位置网络中,可以做出任意分辨率的图像。CPPN 网络的参数-权重与偏差决定产生什么样的图像。根据 CPPN 所选择的架构,所得到的图像中的像素与邻近像素共享颜色在一定程度上受限制。
随机参数可以产生审美直观上感兴趣的图像,但是我们可以通过学习 CPPN 上的参数生产更多有趣的图像,通常这是由进化所完成的。这里,我们研究了反向传播某些目标函数的可能性,例如特征可视化目标。这是很容易就可以做到的,因为 CPPN 网络跟卷积神经网络一样是可微的,并且目标函数同样也可以通过 CPPN 传播从而更新其参数。也就是说,CPPNs 是一种可微化的图像参数化–一种在任何神经艺术或可视化任务中参数化图像的通用工具
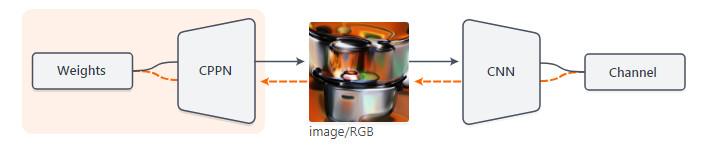
6 : CPPNs 是一个可微的图像参数化,我们可以通过反向传播传递图像将其应用于神经网络艺术或可视化任务,通过 CPPNs 得到其参数。
使用 CPPNs 作为图像参数化能够为神经网络艺术增添一种有趣的艺术品质,让我们朦胧的联想到光绘。(注意,这里光绘的隐喻是比较模糊的:例如光的合成是一个加法过程,而 CPPNs 可以在层与层之间由负的权重连接。更理论层面说,它们可以被视为约束你图像合成复杂度的因素。当用于优化特征可视化目标时,它们生成了不同的图像。)光绘是一种通过棱镜和镜子控制彩色光束从而产生图像的艺术媒介。这种技术典型的应用就是 Stephen Knapp 的作品。
7:CPPN 作为一种可微的图像参数化用于不同层之间的特征可视化。
所生成的图片的视觉质量受到所选择的 CPPN 的架构的影响,不仅是网络的形状(即层和滤波器的数目起到了作用),而且还跟所选择的激活函数与归一化有关。例如,较深的网络比较浅的网络产生更多细微的成分。我们鼓励读者通过改变 CPPN 的架构来生成不同的图像,如果想尝试的话可以通过修改附录中的代码就能轻易地完成。
CPPN 所产生的模式演变就是艺术的产物。为了保持光绘的寓意,优化过程应该考虑光束方向和形状迭代的调整。例如,因为迭代变化相比于像素参数化更有全局影响。在优化开始时,只有主要模式是可见的,通过迭代调整权重,我们想象的光束就会以更完整的细节出现在相应的位置上。
8:训练期间 CPPNS 的输出。在移动设备上你可以通过盘旋或者轻拍的方式来控制每一个视频。
通过这些隐喻,我们可以创造一种能够从上述图片中的任意一张变换成不同图片的新类型动画。直观地说,我们通过 移除光影雕塑上的光束来创造新的图像。事实上,这个结果是通过内插两种不同模式的 CPPN 权重表达式来实现的。然后在给定内插 CPPN 表示法的情况下生成图像从而得到多个中间框架。和之前一样,参数的变化具有全局性,并创造视觉上令人满意的中间框架。
9:在两个已知点中间插入 CPPN 权重
在本小节中,我们提出了一种超标准图像表示的参数化。针对给定目标函数优化的图像,神经网络(在这种情况下为 CPPN)可用于参数化。更确切地说,我们将特征可视化目标函数与 CPPN 参数化相结合,来创造具有独特视觉风格的无限分辨率图像。
第四部分:生成半透明图案
本篇文章中使用的神经网络被训练用来接收 2D RGB 图像作为输入。是否可以用类似的网络来合成超出这种模式的工件呢?事实证明利用可微分参数化定义一系列图像而不是单一图像,然后在每一个优化步骤从系列中取一个或者若干图片作为样本可以实现。这非常重要,因为我们接下来探索优化的许多对象,在进入网络时比图片有着更多的层级和自由度。