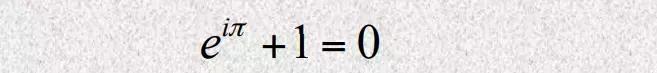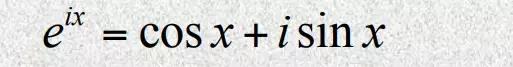在学习与科研中,经常会遇到一些数学运算问题,使用计算机完成运算具有速度快和准确性高的优势。Python的Numpy包具有强大的科学运算功能,且具有其他许多主流科学计算语言不具备的免费、开源、轻量级和灵活的特点。本文使用Python语言的NumPy库,解决数学运算问题中的线性方程组问题、积分问题、微分问题及矩阵化简问题,结果准确快捷,具有一定的借鉴意义。
SymPy一个用于符号型数学计算(symbolic mathematics)的Python库。它旨在成为一个功能齐全的计算机代数系统(Computer Algebra System,CAS),同时保持代码简洁、易于理解和扩展。SymPy完全是用Python写的,并不需要外部的库。
首先,我们通过pip安装一下sympy这个计算库吧!
私信小编007即可获取数十套PDF哦!
pip install sympy
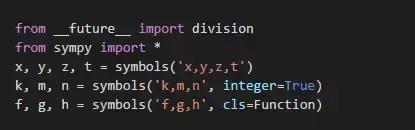
可用SymPy进行数学表达式的符号推导和演算。可使用isympy运行程序,isympy在 IPython的基础上添加了数学表达式的直观显示 功能。启动时还会自动运行下面的程序:
这段程序首先将Python的除法操作符“/” 从整数除法改为普通除法。然后从SymPy库载 入所有符号,并且定义了四个通用的数学符号x 、y、z 、t,三个表示整数的符号k、m、n, 以及三个表示数学函数的符号f、g、h。
欧拉恒等式
此公式被称为欧拉恒等式,其中e是自然 常数,i是虚数单位, 是圆周率。此公式被誉 为数学中最奇妙的公式,它将5个基本数学常数 用加法、乘法和幂运算联系起来。 从SymPy库载入的符号中,E表示自然常 数,I表示虚数单位,pi表示圆周率,因此上面 的公式可以直接如下计算:
print(E**(I*pi)+1)
输出结果为:0
SymPy除了可以直接计算公式的值之外, 还可以帮助做数学公式的推导和证明。欧拉恒等 式可以将 代入下面的欧拉公式得到:
在SymPy中可以使用expand()将表达式展 开e^ix,用它展开看(expand()中x是复数):
print(expand(exp(I*x), complex=True) )
输出:
为了指定x为实数,需要重新定义x
x = Symbol(“x”, real=True)
print(expand(exp(I*x), complex=True))
输出:
数学表达式
创建一个符号使用symbols(),此函数会 返回一个Symbol对象,用于表示符号变量, 其有name属性,这是符号名,如:
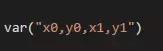
x0=symbols(‘x0’)
其中左边的x是一个符号对象,而右边括 号中用引号包着的x是符号对象的name属性, 两个x不要求一样,但是为了易于理解,通常将 符号对象和name属性显示成一样,另外name 属性是引号包起来的。如要同时配置多个符号 对象,symbols()中多个name属性可以以空格或者逗号分隔,然后用引号包住,如下:
一次配置三个符号,由于符号对象名和 name属性名经常一致,所以可以使用var() 函数,如:
上面的语句创建了名为x0、y0、x1、y1的4 个Symbol对象,同时还在当前的环境中创建 了 4个同名的变量来分别表示这4个Symbol对象。 因为符号对象在转换为字符串时直接使用它的 name 属性,因此在交互式环境中看到变量,x0的 值就是x0,但是査看变量x0的类型时就可以发现 ,它实际上是一个Symbol对象。
type(x0)
数学公式中的符号一般都有特定的假设,例 如m、n通常是整数,而z经常表示复数。在用 var()、symbols()或Symbol()创建Symbol对 象时,可以通过关键字参数指定所创建符号的假 设条件,这些假设条件会影响到它们所参与的计 算。
例如,下面创建了两个整数符号m和n, 以 及一个正数符号x:
每个符号都有许多is_*属性,用以判断符 号的各种假设条件。
SymPy的表达式实际上是一个由Basic类 的各种对象进行多层嵌套所得到的树状结构。 下面的函数使用递归显示这种树状结构:
除了使用SymPy中预先定义好的具有特殊 运算含义的数学函数之外,还可以使用 Function()创建自定义的数学函数:
f = Function(“f”)
当我使用f创建一个表达式时,就相当于创 建它的一个实例:
t = f(x,y)
isinstance(t, Function)
t.func
f的实例t可以参与表达式运算:
t+t*t
f(x, y)**2 + f(x, y)
表达式变换和化简
simplify()可以对数学表达式进行化简:
simplify((x+2)**2 – (x+1)**2)
输出:2*x + 3
radsimp()可以对表达式进行分母有理化,它所得到的表达式分母将没有无理数:
radsimp(1/(sqrt(5)+2*sqrt(2)))
输出:(-sqrt(5) + 2*sqrt(2))/3
fraction()获得ratsimp()通分之后的分子或分母(它不能自动对表达式进行通分):
fraction(ratsimp(1/x+1/y))
输出:(x + y, x*y)
cancel()对分式的分子分母进行约分计算(不能对内部函数的表达式进行约分):
cancel((x**2-1)/(1+x))
输出:x-1
cancel(sin((x**2-1)/(1+x)))
输出:sin(x**2/(x + 1) – 1/(x + 1))
trigsimp()是用来对三角函数进行化简用的:
trigsimp(sin(x)**2+2*sin(x)*cos(x)+cos(x)**2)
输出:sin(2*x) + 1
expand_trig()展开三角函数表达式:
expand_trig(sin(2*x+y))
输出:(2*cos(x)**2 – 1)*sin(y) + 2*sin(x)*cos(x)*cos(y)
log()展开乘积和幂运算:
x,y=symbols(“x,y”,positive=True)
expand(log(x*y**2))
输出:log(x) + 2*log(y)
factor()对多项表达式进行因式分解:
factor(15*x**2+2*y-3*x-10*x*y)
输出:(3*x – 2*y)*(5*x – 1)
integrate()可以用来计算积分,它包含定积分和不定积分:
integrate(f,x):计算不定积分∫ fdx
integrate(f,(x,a,b)):计算定积分∫a/b fdx
当然有时候我们也有多重积分要运算,不要担心,我们还可以用
Integrate(f,x,y)来计算双重积分:∫ ∫ fdxdy
Integrate(f,(x,a,b),(y,c,d)):计算双重定积分(x上下限ab,y上下限cd)
输出:-x*cos(x) + sin(x))
当然,sympy还可以求极限,我们大学学的第一个内容!
语法:limit(function, variable, point),如果是求趋于0,那就把第三个变量改成0,limit(f,x,0),如果是求趋于无穷,第三个变量改成oo(字母)limit(sin(x)/x, x, oo)
输出:1
输出:0
其他还有一些求导,矩阵的算法,平面几何算法,详细见一下sympy文档,这里因为时间问题,我们就不再去介绍了,有问题的可以私聊小编!
高数计算,我Python替你承包了http://t.jinritoutiao.js.cn/e7jMn6/
转载请注明:徐自远的乱七八糟小站 » 高数计算,我Python替你承包了