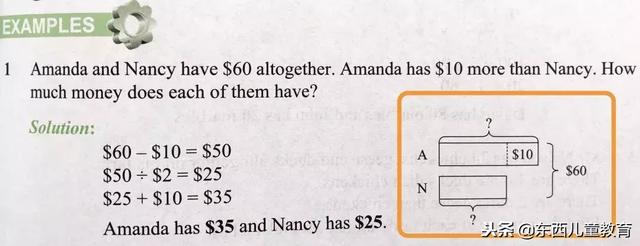今天这篇分享，可以算是我之前写的一篇《花5分钟，把全球排名第一的新加坡数学精髓学回去，辅导孩子超管用！》的续集。

在那篇文章里，我为大家介绍了新加坡数学里的“Model Drawing”建模方法，这里我先简单总结一下，之前没读过的同学就不用回翻了。

建模可以说是新加坡数学的核心精髓。

不过大家不用把它想成我们高中大学时参加的数学建模竞赛，没那么复杂，但思想是类似的，就是想办法用固定的、规整的模型来描述一个现实问题，这样，对现实问题的思考就转化成对这个模型的研究。最常用的建模方法是Bar Model，就是下面这种方框图，我们看两个用建模方法来解应用题的简单例子：

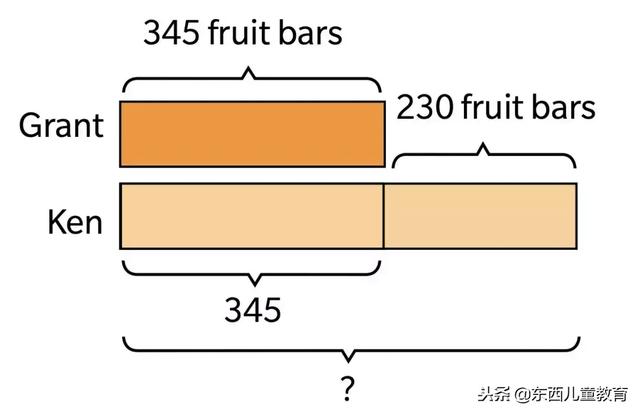
Grant 有345个水果派，Ken比Grant多230个，问Ken有多少个水果派？

Amanda和Nancy一共有60块钱，Amanda的钱比Nancy多10块，问她们各有多少钱？

方法很简单，就一个关键点，用不同长度的方框表示数量，画的时候尽量符合比例，这样孩子在用建模方法解答的过程中，对数量的大小，数量之间的关系就会有很直观的感受。

很多孩子觉得数学困难，往往是因为从具体到抽象这关过不好，刚开始数学启蒙时可以掰手指，数积木块，这时的数学是具象的，在生活中可见的。但后面一上到抽象的数字符号，运算公式时，数学就变成一门看不见摸不着的学科了，不适应的孩子很容易产生畏惧心理。

而建模用的方框图，就相当于从具体实物到抽象符号中间的桥梁。新加坡数学把这种方法称为“CPA教学法”，最早是美国心理学家杰罗姆 · 布鲁纳提出来的，他经过长期的研究观察发现，孩子学习要经历三个阶段：C – Concrete 具象化、P – Pictorial 形象化、A – Abstract 抽象化。

对应地，从具体实物（积木块），到抽象的数学算式（2+1=3），中间需要有一个“形象化”的过渡，就是建模。

看起来很简单对吧？

但后来我发现，建模的意义还远不仅在于帮助孩子从具体过渡到抽象，更关键的是，经常练习、懂得熟练运用的话，它能让孩子养成“把复杂问题形象化、简化”的思维习惯。

今天要分享的就是一次我被逃逃用建模“打败”的经历。

我家陪娃做数学作业（需要陪的也几乎都是我们自己课外给他布置的）时有个特点，无论是我陪还是逃爸陪，都喜欢跟逃逃一起做同样的题，一来一起做题他就特来劲儿，常常上纲上线地要跟我们比比速度、正确率啥的，很有正向激励作用；二来我们跟着做熟悉一下题型思路，如果他有什么搞不懂的，也能马上辅导得上。当然我们也是自恃当年数学还不错，对一些需要动点脑筋，有些挑战的数学题也很感兴趣。

这是我和逃逃一起做的一道题：

我先翻译并简化一下：

一人叫C，一人叫P，他们手上都有些卡片。一开始C的卡片数是P的5倍。然后，C把自己的1/4给了P，P收下之后又把自己目前总拥有的1/3给了C。现在，C的卡片比P多96张。问一开始C有多少张卡片？

咋一看挺复杂，卡片给过来给过去的，有点儿头大。我知道用一元一次方程肯定能解出来，但直觉应该有更好的方法，正在思考中发现逃逃已经刷刷刷地在草稿纸上涂涂写写了。我心想不能落后，索性就用方程吧，反正他在准备AMC8的数学竞赛里也接触过方程了，应该不会觉得我耍赖～

于是我开始按部就班地算，假设一开始P的卡片数量是p的话，那么，他们俩初始卡片数量分别是，

C把自己的1/4给了P之后，他们的卡片数量变成，

P收下之后又把自己目前总拥有的1/3给C，所以这时他们的卡片数量就变成，

现在C的卡片比P多36张，也就是说，

好长的算式，但肯定是可以算出来的嘛，于是我就继续一步一步往下走。还没算到一半的时候，逃逃在旁边喊“Done”（搞定！）。

我心想，哼，让你图快，一会儿看谁算得对。

我于是飞快地计算，然后和他对答案，我俩的答案一样，都是160。

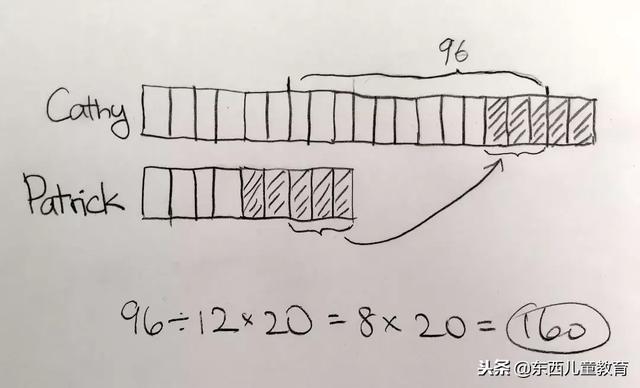
逃逃看了看我的草稿纸，摇摇头“对是对的，不过这方法有点儿笨啊”，然后得意洋洋得给我秀他的方法：

啊，对呀！用建模图，我怎么没想到？！

我一下恍然大悟，为了让他攒足成就感，我开始作虚心听讲状（对了，这招很管用，跟孩子认怂，让他给你讲讲，他讲的过程也是他再次理清思路的过程，不过这次我是真怂，不是故意的～）

然后逃逃就开讲，他讲得还挺细致的（为了让大家看得比较清楚，以下我重新用电脑画图来说明一下过程）：

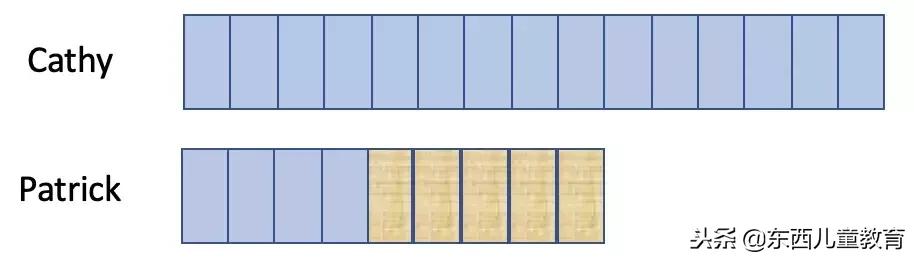
1. 一开始他们俩拥有的卡片数量是1:5，C的数量是P的5倍，可以这么表示：

2. C把自己的1/4给P，但是C现在被分成5份，怎么取1/4呢？没关系，把每一份都分成4小格，每一份中取一小格出来，就是1/4了。相应的，我们也把P分成4小格：

3. C把1/4，也就是上面标黄的5个小格给了P后，他们俩的数量就是这样：

4. P再把自己的1/3给C，就变成了这样：

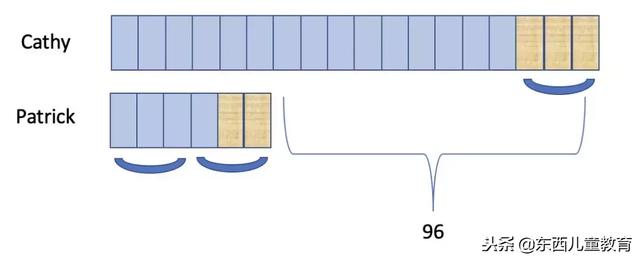
到这里就很清楚了，C比P多了12小格，这12小格是96张，所以每一小格是96/12=8张。那么C一开始是有20小格的，所以一开始Cathy拥有的卡片数量就是8*20=160张。

哇，是挺简捷的！

但我依然有点不服气，说他算是走运，因为到最后一步P有9小格，而刚好是要分1/3，如果要分1/4不就坏菜了吗？逃逃说没关系啊，你就再继续分格子啊，每小格分四份，和第2步的方法一样啊……想想的确可行，而且小学数学重在培养思维，人家题目也不会特意在数值上搞得太复杂，我也不再钻牛角尖了。

而且，两种方法的对比中，我发现很关键的一点，在用建模画图时，孩子心中是一直有数量的概念在的，C和P之间的数量对比关系，是怎么交互、变化的，一清二楚，这对培养孩子的数感很有帮助，能让孩子养成把复杂问题形象化、简化的思维习惯。

不过，这种习惯要靠长期的练习，因为逃逃长期在用新加坡数学的练习册，我发现它有个特点，很多重要的知识点和方法是循环递进地训练，比如这个建模方法，每个年级都会练，但难度逐年往上走一点点。

比如学前班阶段会借助实物教具：

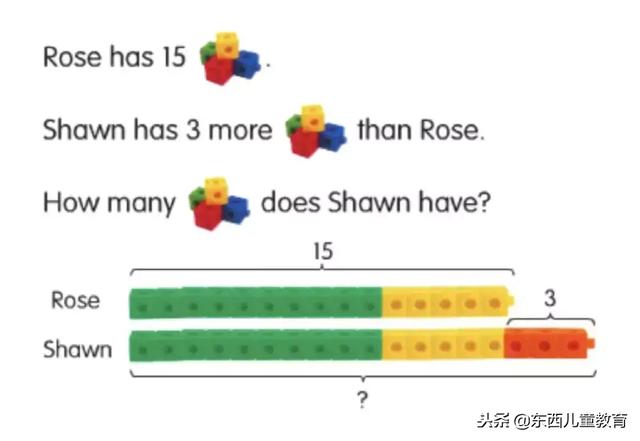
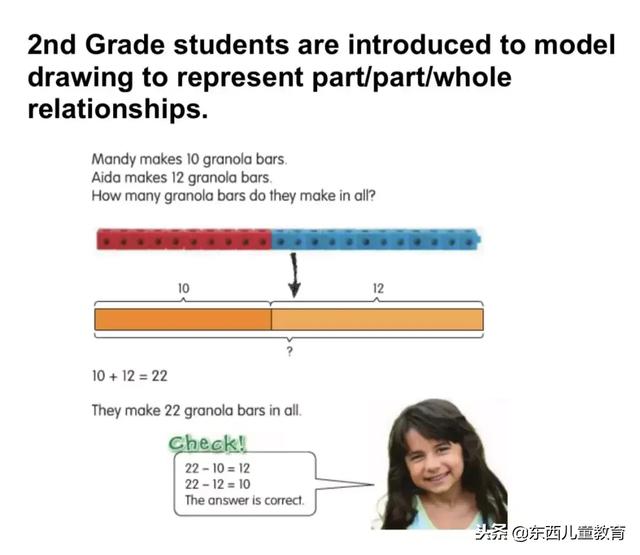
到了1、2年级，从实物过渡到建模图：

开始解决简单的问题：

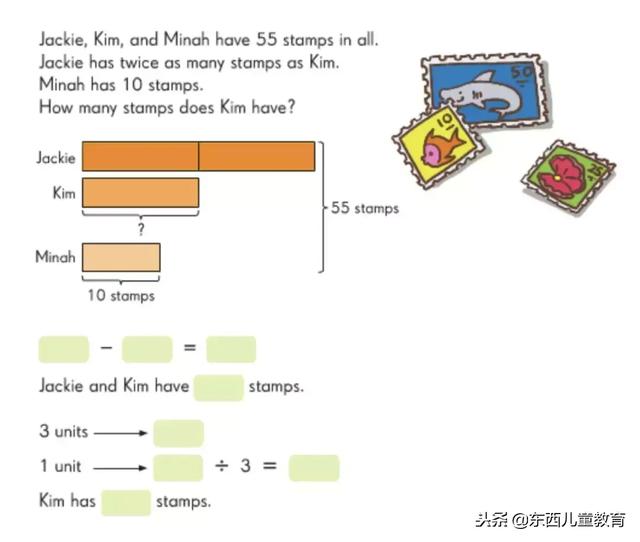
而3、4年级之后，会用建模来解决更复杂的问题：

即便是到了学方程，依然会用建模来辅助理解，比如下面这个简单的二元一次方程：

x+y=7

x+2y=11

用建模图来表示如下，能非常清楚地看到两个式子的比较关系，是不是对x和y的数量理解更形象了？

我发现，这个“Model Drawing”建模方法之所以威名远扬，被称之为新加坡数学的核心精髓，不仅在于方法本身，更重要的是，它还被细化到每个年级，循环递进，成为一整套辅助和帮助孩子掌握、理解、灵活运用的训练体系，这个非常有价值。

毕竟搞明白是一回事，而能否熟练运用，养成一种把复杂问题形象化、简化的思维习惯又是另一码事了，这之间的gap就是要多练，而且是循环递进，有针对性的练习。

虽败，但很服气！

我之前整理过一份帮助家长理解学习和辅导孩子的材料，这次新增了不少内容，有需要的同学可以私信我回复“新加坡数学”即可获得。

我引以为豪的数学，被娃用新加坡数学打败了！http://t.jinritoutiao.js.cn/8KY52A/

转载请注明：徐自远的乱七八糟小站 » 我引以为豪的数学，被娃用新加坡数学打败了！