卷积到底是什么?今天让你彻底明白
读本科期间,信号与系统里面经常讲到卷积(convolution),自动控制原理里面也会经常有提到卷积。硕士期间又学了线性系统理论与数字信号处理,里面也是各种大把大把卷积的概念。至于最近大火的深度学习,更有专门的卷积神经网络(Convolutional Neural Network, CNN),在图像领域取得了非常好的实际效果,已经把传统的图像处理的方法快干趴下了。啰啰嗦嗦说了这么多卷积,惭愧的是,好像一直以来对卷积的物理意义并不是那么清晰。一是上学时候只是简单考试,没有仔细思考过具体前后的来龙去脉。二是本身天资比较愚钝,理解能力没有到位。三则工作以后也没有做过强相关的工作,没有机会得以加深理解。趁着年前稍微有点时间,查阅了一些相关资料,力争将卷积的前世今生能搞明白。
首先选取知乎上对卷积物理意义解答排名最靠前的回答。
不推荐用“反转/翻转/反褶/对称”等解释卷积。好好的信号为什么要翻转?导致学生难以理解卷积的物理意义。
这个其实非常简单的概念,国内的大多数教材却没有讲透。
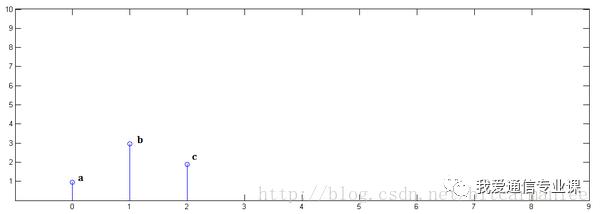
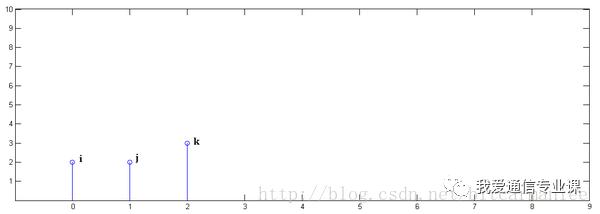
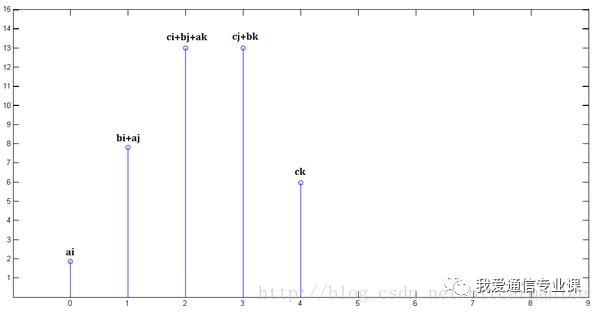
直接看图,不信看不懂。以离散信号为例,连续信号同理。
已知x[0] = a, x[1] = b, x[2]=c
已知y[0] = i, y[1] = j, y[2]=k
下面通过演示求x[n] * y[n]的过程,揭示卷积的物理意义。
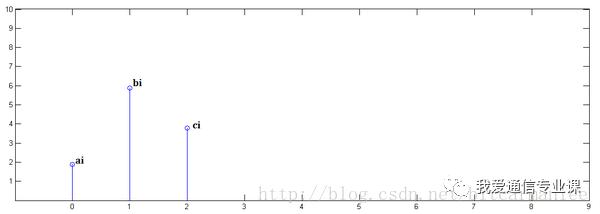
第一步,x[n]乘以y[0]并平移到位置0:
第二步,x[n]乘以y[1]并平移到位置1
第三步,x[n]乘以y[2]并平移到位置2:
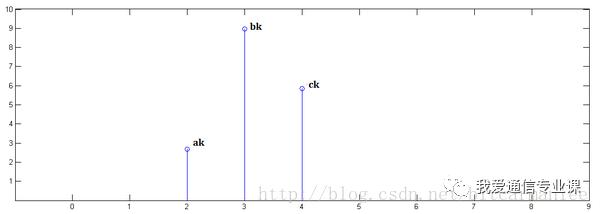
最后,把上面三个图叠加,就得到了x[n] * y[n]:
简单吧?无非是平移(没有反褶!)、叠加。
从这里,可以看到卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数(如:输入信号)上的加权叠加。
重复一遍,这就是卷积的意义:加权叠加。
对于线性时不变系统,如果知道该系统的单位响应,那么将单位响应和输入信号求卷积,就相当于把输入信号的各个时间点的单位响应 加权叠加,就直接得到了输出信号。
通俗的说:
在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。
这正是单位响应是如此重要的原因。
卷积到底是什么?今天让你彻底明白http://t.jinritoutiao.js.cn/dysCHQ/
转载请注明:徐自远的乱七八糟小站 » 卷积到底是什么?今天让你彻底明白