【从0到1-11-74行Python实现手写体数字识别】
到目前为止,我们已经研究了梯度下降算法、人工神经网络以及反向传播算法,他们各自肩负重任:
- 梯度下降算法:机器自学习的算法框架;
- 人工神经网络:“万能函数”的形式表达;
- 反向传播算法:计算人工神经网络梯度下降的高效方法;
基于它们,我们已经具备了构建具有相当实用性的智能程序的核心知识。它们来之不易,从上世纪40年代人工神经元问世,到80年代末反向传播算法被重新应用,历经了近半个世纪。然而,实现它们并进行复杂的数字手写体识别任务,只需要74行Python代码(忽略空行和注释)。要知道如果采用编程的方法(非学习的方式)来挑战这个任务,是相当艰难的。
本篇将分析这份Python代码“network.py”,它基于NumPy,在对50000张图像学习后,即能够识别0~9手写体数字,正确率达到95%以上。强烈建议暂时忘记TF,用心感受凝结了人类文明结晶的沧桑算法。代码来自Micheal Nielsen的《Neural Networks and Deep Learning》,略有修改(格式或环境匹配),文末有下载链接。
MNIST数据集
MNIST
早在1998年,在AT&T贝尔实验室的Yann LeCun就开始使用人工神经网络挑战数字手写体识别,用于解决当时银行支票以及邮局信件邮编自动识别的需求。而现今,数字手写体识别,已经成了机器学习的入门实验案例。算法实验使用最广泛的数据集就是MNIST,由Yann LeCun提供下载。它包含了60000张训练图片集,以及10000张测试图片集,最初来源于NIST(National Institute of Standards and Technology,美国国家标准与技术研究院)数据库。
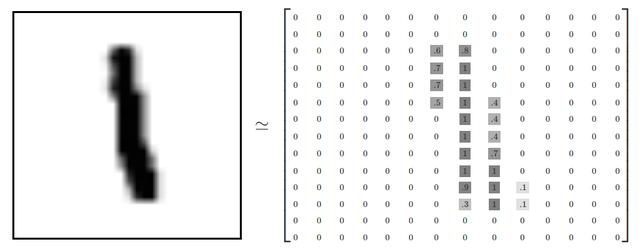
样本图像
如上图所示,MNIST中的图像是灰度图像,像素值为0的表示白色,为1的表示黑色,中间值是各种灰色。每张样本图像的大小是28×28,具有784个像素。
训练集与测试集
MNIST中的60000张训练图像扫描自250个人的手写样本,他们一半是美国人口普查局的员工,一半是大学生。10000张测试图像来自另外250个人(尽管也是出自美国人口普查局和高校)。可是为什么要这么做呢?答案是为了泛化(Generalization)。
人们希望学习训练集(training set)后获得的模型,能够识别出从未见过的样本,这种能力就是泛化能力,通俗的说,就是举一反三。基于这种考虑,测试集(test set)不会参于模型的训练,而是特意被留出以测试模型的泛化性能。周志华的西瓜书中有一个比方:如果让学生复习的题目,就是考试的考题,那么即便他们考了100分,也不能保证他们真的学会了。
标签
Label
上图中右侧的部分,称为标签(Label),是和样本数据中的每张图片一一对应的,由人工进行标注。标签是数据集必不可少的一部分。模型的训练过程,就是不断的使识别结果趋近于标签的过程。基于标签的学习,称为有监督学习。
验证集与超参数
来自Micheal Nielsen的代码,又把60000张训练集进行了进一步的划分,其中50000张作为训练集,10000张作为验证集(validation set)。所以代码使用MNIST数据集与Yann LeCun的是有些区别的,本篇使用的MNIST从这里下载。
模型的参数是由训练数据自动调整的,但是还有不被学习算法覆盖的参数,比如神经网络中的学习率等,它们被称为超参数。验证集就是用于优化超参数的。尽管验证数据不是MNIST规范的一部分,但是留出验证数据已经成了一种默认的做法。
Python必知必会:张量构建
本篇使用与《Neural Networks and Deep Learning》示例代码一致的Python版本:
- Python 2.7.x,使用了conda创建了专用虚拟环境,具体方法参考1 Hello, TensorFlow!;
- NumPy版本:1.13.1。
作为AI时代头牌语言的Python,具有非常好的生态环境,其中数值算法库NumPy做矩阵操作、集合操作,基本都是“一刀毙命”。为了能顺畅的分析接下来的Python代码,我挑选了1处代码重点看下,略作修改(前两层神经元数量)可以单独运行。
|
1 |
1 import numpy as np2 sizes = [8, 15, 10] |
第1行:导入numpy并启用np作为别名。
第2行:是一个数组定义,其中包含了3个元素。
第3行:
- 先看
sizes[1:],它表示sizes的一个子数组,包含元素从原数组的下标1开始,直到原数组最后1个元素,它的值可以算出是[15, 10]; - 然后是NumPy的随机数生成方法
random.randn,它生成的随机数,符合均值为0,标准差为1的标准正态分布; random.randn方法的参数,描述生成张量的形状,例如random.randn(2,3)会生成秩为2,形状为shape[2,3]的张量,是一个矩阵:array([[-2.17399771, 0.20546498, -1.2405749 ], [-0.36701965, 0.12564214, 0.10203605]]),关于张量请参考2 TensorFlow内核基础;- 第3行整体来看才能感受到Python和NumPy的威力:方法参数的参数化,即调用
randn方法时可传入变量:randn(y, 1),而变量y遍历集合sizes[1:],效果等同于[randn(15, 1), randn(10, 1)];
第4行:
- 先看
sizes[:-1]表示其包含的元素从原数组的第1个开始,直到原数组的最后1个的前一个(倒数第2个),此时sizes[:-1]是[8, 15]; - 第4行
randn的两个参数都是变量y和x,此时出现的zip方法,限制了两个变量是同步自增的,效果等同于[randn(15, 8), randn(10, 15)]。
矩阵与神经网络
分析了前面4行代码,我们知道了如何高效的定义矩阵,但是和神经网络的构建有什么关系呢?下面给出网络结构与矩阵结构的对应关系。
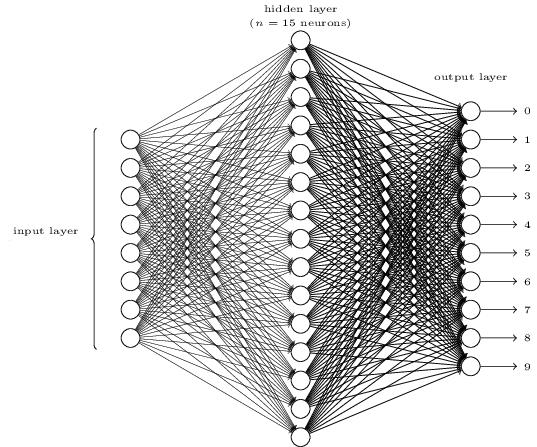
3层感知器
上面的神经网络结构即可描述为:sizes = [8, 15, 10],第一层输入层8个神经元,第二层隐藏层15个神经元,第三层输出层10个神经元。
第一层是输入层,没有权重和偏置。
第二层的权重和偏置为:
第2层神经元的权重和偏置
第三层的权重和偏置为:
第3层神经元的权重和偏置
回看第3行代码,其等价于[randn(15, 1), randn(10, 1)],相当于把网络中的两层偏置矩阵放在一起了:
|
1 |
3 biases = [np.random.randn(y, 1) for y in sizes[1:]] |
回看第4行代码,其等价于[randn(15, 8), randn(10, 15)],相当于把网络中的两层权重矩阵放在一起了:
|
1 |
4 weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] |
而这4个矩阵本身,就代表了想要构建的神经网络模型,它们中的元素,构成了神经网络的所有可学习参数(不包括超参数)。当明了了神经网络与矩阵群的映射关系,在你的脑中即可想象出数据在网络中的层层流动,直到最后的输出的形态。
随机梯度下降算法框架
整个神经网络程序的骨架,就是梯度下降算法本身,在network.py中,它被抽象成了一个单独的函数SDG(Stochastic Gradient Descent):
|
1 |
def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None) |
函数体的实现,非常清晰,有两层循环组成。外层是数据集的迭代(epoch);内层是随机梯度下降算法中小批量集合的迭代,每个批量(batch)都会计算一次梯度,进行一次全体参数的更新(一次更新就是一个step):
|
1 |
for j in range(epochs): random.shuffle(training_data) |
BP
可以想象self.update_mini_batch(mini_batch, eta)中的主要任务就是获得每个参数的偏导数,然后进行更新,求取偏导数的代码即:
|
1 |
delta_nabla_b,delta_nabla_w = self.backprop(x, y) |
反向传播算法(BP)的实现也封装成了函数backprop:
|
1 |
def backprop(self, x, y): """Return a tuple ``(nabla_b, nabla_w)`` representing the |
识别率
运行代码,在Python命令行输入以下代码:
|
1 |
import mnist_loader |
上面代码中的mnist_loader负责MNIST数据的读取,这部分代码在这里下载,为了适配数据集的相对路径做了微调。
接下来,定义了一个3层的神经网络:
- 输入层784个神经元(对应28×28的数字手写体图像);
- 隐藏层30个神经元;
- 输出层10个神经元(对应10个手写体数字)。
最后是梯度下降法的设置:
- epoch:30次;
- batch:10个样本图像;
- 学习率:3.0。
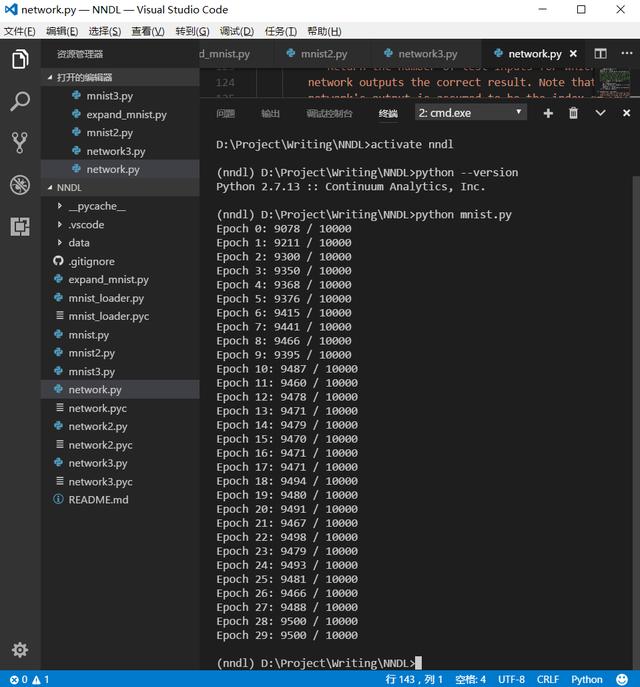
代码开始运行,30次迭代学习后,识别准确率即可达到95%。这个识别率是未去逐个优化超参数,就能轻松得到的,可以把它当做一个基线水准,在此基础上再去慢慢接近NN的极限(99.6%以上)。
运行结果如下:
识别准确率
附完整代码
|
1 |
""" |
看到一位大牛写的 好厉害,所以就拿出来给大家分享一下,程序还是需要多写,多思考多变化。代码多敲就熟练了,不管天赋怎样,勤能补拙嘛,大家可以加我python交流群:58937142,里面新手资料,框架,爬虫。web都有,都是可以免费获取的,还有大牛解答各种难题,不失为是一个学习的好地方,小编在这里邀请大家加入我的大家庭。欢迎你的到来。