【「Python破解九宫格数独」:九宫格生成与数独求解】
作者:冰不语
来源:「CVPy」公众号
前言
在此之前,OpenCV玩九宫格数独(一)和OpenCV玩九宫格数独(二)分别介绍了如何从九宫格图片中提取出已知数字和如何用knn训练数字识别模型。在这些前期工作都已经完成的基础上,接下来我们需要做什么呢?
我们要做的有三部分:
1.生成九宫格,也就是生成一个9×9的矩阵,把已知的数字按照图片中的位置填到矩阵中的相应位置,其他位置全部置0。
2.编写数独求解算法,对九宫格矩阵进行求解。
3.把填完的九宫格重新填充到图片中去。
我们仍然是一步一步来说。
生成九宫格
这里就需要用到我们之前两篇的内容了,生成九宫格的步骤如下:
1.从九宫格图片中提取数字(第一篇内容)
2.用训练的数字识别模型对上一步的数字进行识别。
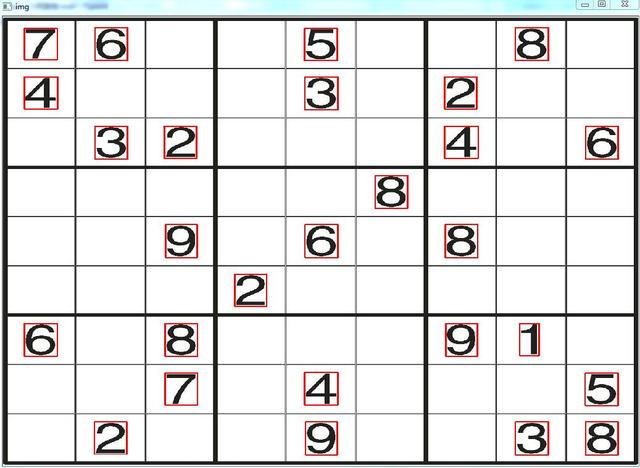
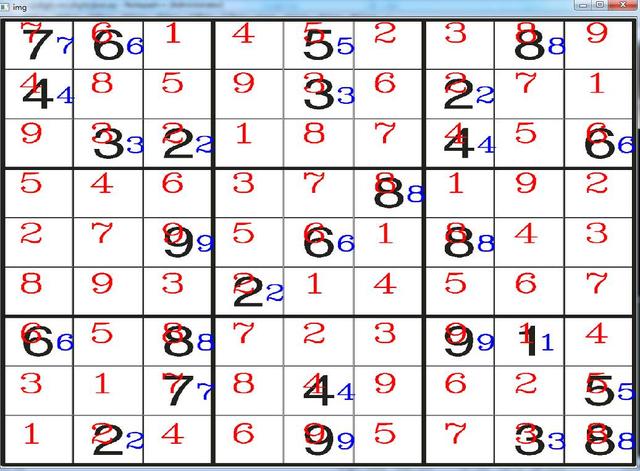
这里需要注意的是,提取之后的数字,要按照训练模型之前的数据处理方式进行处理,然后输入knn模型识别。识别效果如下图所示。就像上一篇结尾说的一样,本文用不到一百个样本训练出来的模型仅仅能保证在本文的示例图片上取得完美效果。其他情况下不作保证。如果想要得到更完美的数字识别模型,请优化数据预处理方式和加大数据量。
3.按照位置顺序把数字填入相应的矩阵位置中。
矩阵初始化为零阵
soduko = np.zeros((9, 9),np.int32)
然后按照位置求解数字在矩阵中所处的位置
## 求在矩阵中的位置soduko[int(y/box_h)][int(x/box_w)] = number
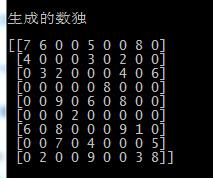
得到的矩阵如下所示:
跟上面的图片比较一下,是不是位置一样呢?
编写算法求解九宫格矩阵
数独的求解算法有很多种,热爱数独的且热爱数学的人对此进行了深入研究,提出了各种各样的算法。这里用的是传说中的回溯法。回溯法具体内容感兴趣的可以自行搜索,我这里只是用,没有深究。
至于为什么用这个算法?。。。因为我在stackoverflow上找到了可用的代码(捂脸逃…)
代码里标注了出处:
## 数独求解算法,回溯法。来源见下面链接,有细微改动。## http://stackoverflow.com/questions/1697334/algorithm-for-solving-sudokudef findNextCellToFill(grid, i, j):for x in range(i,9):for y in range(j,9):if grid[x][y] == 0:return x,yfor x in range(0,9):for y in range(0,9):if grid[x][y] == 0:return x,yreturn -1,-1def isValid(grid, i, j, e):rowOk = all([e != grid[i][x] for x in range(9)])if rowOk:columnOk = all([e != grid[x][j] for x in range(9)])if columnOk:# finding the top left x,y co-ordinates of the section containing the i,j cellsecTopX, secTopY = 3 *int(i/3), 3 *int(j/3)for x in range(secTopX, secTopX+3):for y in range(secTopY, secTopY+3):if grid[x][y] == e:return Falsereturn Truereturn Falsedef solveSudoku(grid, i=0, j=0):i,j = findNextCellToFill(grid, i, j)if i == -1:return Truefor e in range(1,10):if isValid(grid,i,j,e):grid[i][j] = eif solveSudoku(grid, i, j):return True# Undo the current cell for backtrackinggrid[i][j] = 0return False
然后我们根据算法对前面生成的数独求解。只需要这么一句就行:
solveSudoku(soduko)
这里为了便于观察,分别 原始数独、求解后的数独,为了验算,输出结果数独的每行每列的和,如果求解正确,每行每列和都应该等于1+2+...+9=45。
print("\n生成的数独\n")print(soduko)print("\n求解后的数独\n")## 数独求解solveSudoku(soduko)print(soduko)print("\n验算:求每行每列的和\n")row_sum = map(sum,soduko)col_sum = map(sum,zip(*soduko))print(list(row_sum))print(list(col_sum))
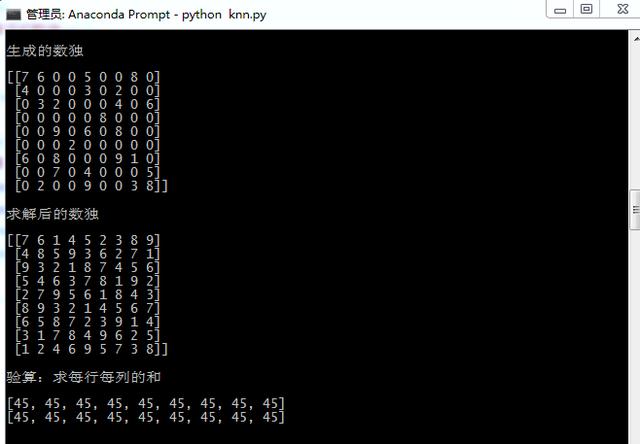
输出的结果如下:
最后两行可以看到各行各列的和确实都是45。数独求解成功。
在黑窗口里看最后的数独可能不那么友好,接下来我们就把生成的九宫格填充到图片里来看。
填充图片九宫格
我们只需要在图片中九宫格中相应的位置写相应的数字就可以了,这一部分乏善可陈。还是直接看代码和效果图吧。
## 把结果按照位置填入图片中for i in range(9):for j in range(9):x = int((i+0.25)*box_w)y = int((j+0.5)*box_h)cv2.putText(img,str(soduko[j][i]),(x,y), 3, 2.5, (0, 0, 255), 2, cv2.LINE_AA)#print(number_boxes)cv2.namedWindow("img", cv2.WINDOW_NORMAL);cv2.imshow("img", img)cv2.waitKey(0)
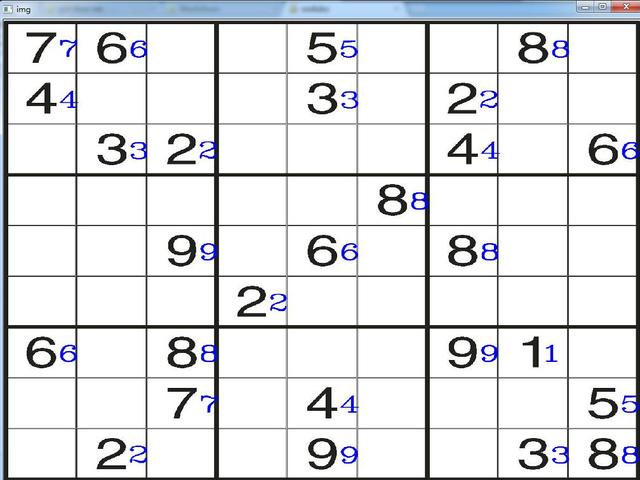
最后的效果你应该在预告篇就看到过了。为了便于对比,保留了上一步数字识别的结果。
尾声
到此,整个opencv玩数独项目告一段落。容我感慨几句。
玩数独项目最早可以追溯到一年前,那时候就开始尝试用C++来对数独图片进行处理,但是最终受限于当时的水平和心态,只完成了一小半。为什么说心态呢?因为那时候很多东西不会的也不敢去尝试,如果当时敢于尝试,畏难心理没有那么重的话,也许这个项目会提前很久完成。
其实我本来最擅长的是C++的,然而最近用python越来越顺手了。这个项目坐下来受益最大的显然是我自己。分享出来,感兴趣的人也许会有很多,但是真正会去做一遍的应该没有几个。会完整做下来的应该更是寥寥无几。
这个小项目都对高手来说也许不算什么,但是对于初学Python和opencv的人来说应该是一个不错的锻炼。希望有人能做一遍,能做下来的相信会做的更好。欢迎感兴趣的人来一起交流学习。
代码
github: https://github.com/LiuXiaolong19920720/opencv-soduko
题图:pexels,CC0 授权。